목차

  • Uncertainty(불확실성)이란?
  • Evidential Deep Learning
    • Background
    • Limitation
  • Fisher Information Evidential Deep Learning($\mathbf{I}$-EDL)
    • Motivaton
    • 문제점
  • t-SNE(t-distribution Stochastic Neihbor Embedding)
    • 아이디어
    • 작동원리
    • 주의사항
  • 예시 코드
  • 결론
  • 참고자료

1. Uncertainty(불확실성)이란?

자율주행, 의학분야에서는 딥러닝의 설명불가능한 측면이 문제가 되는 경우가 많다. 이처럼 특히 사람의 안전이나 생명이 관련된 분야에서는 단순히 예측력이 높은 모델뿐 아니라 설명가능한(explainable) 모델이 필요한 경우가 있는데 이럴 때 그 측도 중 하나로 사용되는것이 불확실성(uncertainty)이다. 우리가 만약 불확실성을 측정할 수 있다면 예컨데, 자율주행 중에 어떤 경우에는 불확실성이 높다면 그 경우에는 주행자에게 경보를 줘 주행자가 직접 운행할 수 있도록 하고, 의학 분야에서도 의사 등의 결정권자에게 경고를 할 수 있을 것이다. 그래서 단순히 예측력이 높은 모델이 아니라 불확실성을 예측할 수 있는 모델을 만드는 것이 중요한데, 그 중 대표적으로 베이지안 뉴럴 네트워크(bayesian nueral network)나 Evidential Deep Learning 등이 있다. 이 포스팅에서는 후자를 주로 다룰 것이다. 그러기 전에 불확실성에 대해서 조금 더 설명하고 넘어가도록 하자.

불확실성에는 크게 aleatroric uncertainty와 epistemic uncertainty 두가지 종류가 있다.

  • Aleatroric uncertainty

Aleatroric uncertainty는 다르게 말하면 data uncertainty 혹은 irreducible uncertainty라고 불리기도 한다. 이는 단어 자체에서도 의미하듯이 자연스러운 불확실성으로 데이터의 수를 늘려도 이를 줄이기는 불가능하다. 예시로는 label noise, measurement noise , missing data등으로 인해 생기는 불확실성 등이 있다.

  • Epistemic uncertainty

Epistemic uncertainty는 model uncertainty 혹은 reducible uncertainty라고 불리기도 한다. 단어자체에서 나타내듯이 lack of knowledege(data) 때문에 생기는 불확실성으로, 이는 데이터의 수를 늘림으로써 불확실성을 줄일 수 있다. 이때 train distribution과 test distribution의 괴리때문에 생기는 OOD(Out of distribution)문제도 epistemic uncertainty로 볼 수 있으나 사람에 따라서는 이건 distribution uncertainty로 따로 분류하는 사람도 있다. 예시를 들어서 설명해보면 개와 고양이를 분류하는 모델을 만든다해서 training set에는 개와 고양이 사진만 있는 data로 model을 학습시켰는데 test시 고양이나 개 사진이 아니라 갑자기 당나귀 사진을 보여준다면 이 경우 softmax로 통과시킨 확률값이 $P(Y=\text{강아지} ㅣx)=0.9$ 라고 매우 높은 confidence로 당나귀를 강아지로 판단하게 될 것이다. 이럴 때 불확실성을 예측가능하다면 이 결과가 믿을만하지 못하단것을 알 수 있을것이다.

Aleatroric uncertainty과 Epistemic uncertainty를 그래프로 표현하면 다음과 같다.

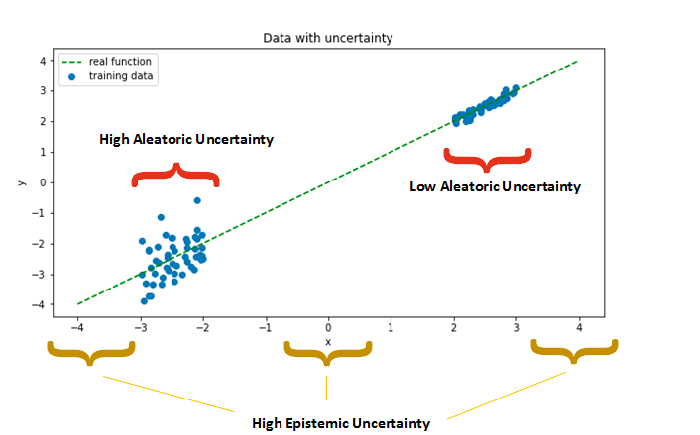
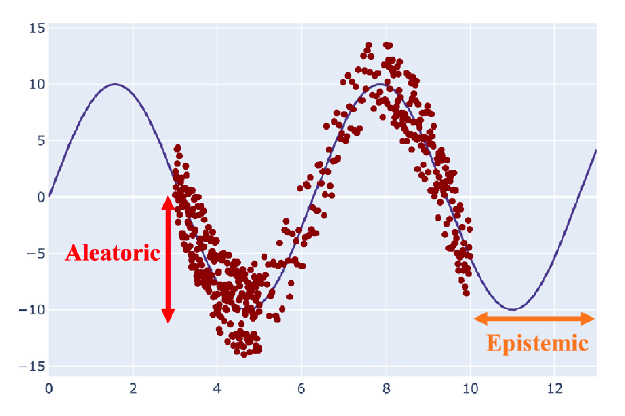
이제 이러한 불확실성들을 예측하려는 모델에 대해서 알아보도록 하자.

2. Evidential Deep Learning

Background

위에서 말한것 처럼 불확실성을 예측하려는 모델 중 대표적으로 BNN과 EDL이 있는데 전자의 경우 딥러닝 모델의 weight 자체에 distribution을 부여해 probablistic model이 되고 후자의 경우에는 weight자체는 deterministic하지만 보통의 DNN이 모델의 마지막 layer에 softmax를 부여해서 $p_{k}$ 를 구하는 것과 달리 EDL의 경우는 모델의 output $\alpha = (\alpha_{1},\, \alpha_{2},\, \cdots, \alpha_{k})$ 를 diriclet분포의 parameter로 사용하여 $p = (p_{1},\, p_{2},\, \cdots, p_{k}) \sim \text{Dir}(\alpha_{1},\, \alpha_{2},\, \cdots, \alpha_{k})$ 로 구한다. 이를 통해서 $p_{k}$ 의 결합분포를 알 수 있는데 그 분포를 통해 불확실성을 예측하는게 가능하다.

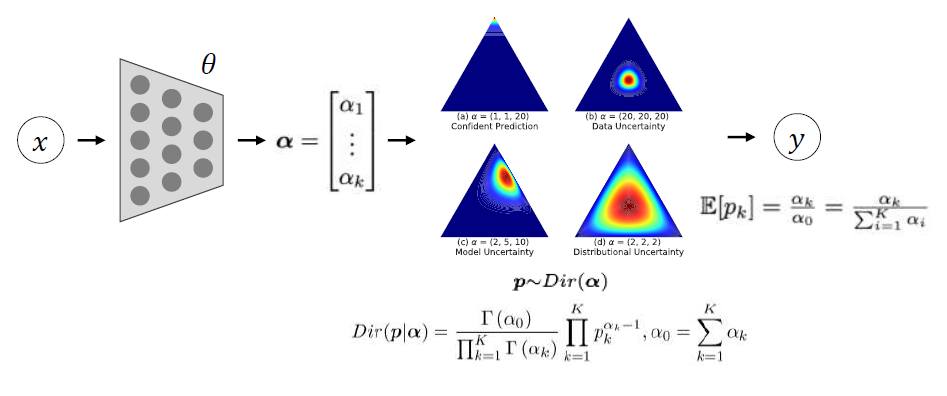
또한 이를 통해 $p_{k}$ 를 예측할 때에는 별도의 sampling과정을 거치거나 하진 않고 $\hat{p_{k}} = \mathbb{E}(p_{k})$ 로 예측값을 정의한다.

이때 위의 경우는 k개의 label을 가지는 분류문제이기 때문에 Diriclet분포를 사용하였는데 만약 회귀문제라면 DNN으로부터는 $(\gamma,\, \nu,\, \alpha,\, \beta )$ 를 뽑아내고 이를 통해서,

\[\begin{aligned} & u \sim \text{Normal}(\gamma, \, \sigma^{2} \nu ^{-1}) \\ & \sigma^{2} \sim \Gamma^{-1} (\alpha,\, \beta) \end{aligned}\]

분포를 사용해 $u$와 $\sigma$를 얻을 수 있고, $y \sim N(u,\, \sigma^{2})$으로 모델을 만들어 $y$를 예측할 수 있다.

이번 포스팅에서는 회귀문제가 아닌 k개의 label을 가지는 분류문제에 한에서만 다루도록 하겠다.

  • 참고: 각각 Diriclet 분포와 NormalInverseGamma 분포를 사용하는 이유는 이것이 각 경우의 conjugate prior이기 때문이라곤 하는데 아직 여기까지 자세하게 공부하진 않아서 잘 모르겠다.

이 경우 한가지 흥미로운 사실은 원래의 경우 분류문제에서는 $y \sim \text{Category}(p)$ 형태의 분포가정을 하는데 이 포스팅의 베이스가 된 논문(Zhang, 2023)에서는 $y ~\sim N(p, \, \sigma^{2} I)$ 분포가정을 한다. 이를 통해 학습과정에서 쓰이는 objective function을 다음과 같이 정의한다.

(Sensoy et al.(2018) paper에 이렇게 정규가정을 해서 loss를 mse를 사용하나 아니면 cross entropy loss를 사용하나 큰 차이가 없음을 경험적으로 밝혔으니 관심있는 사람들은 해당 논문을 찾아보면 좋을것 같다.)

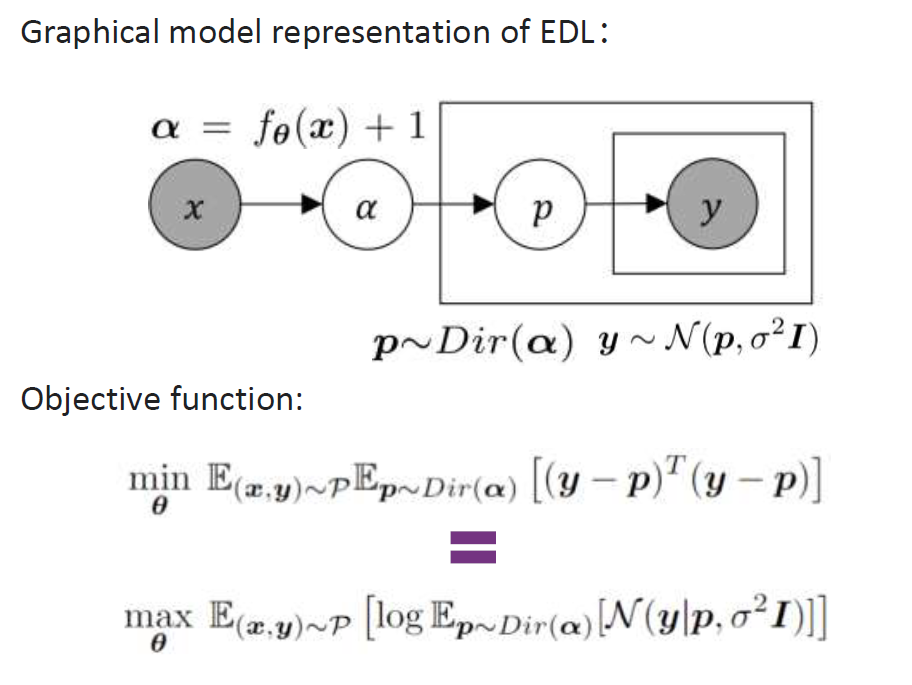
이때 $y ~\sim N(p, \, \sigma^{2} I)$를 사용한 보통의 경우 그 MSE를 최소화 시키는 방향으로 학습을 많이 진행하는데 이는 로그 가능도 함수를 최대화 시키는것과 같음이 알려져 있다. 그래서 위 사진의 제일 아래식으로 최적화를 진행한다. (굳이 이렇게 바꿔 표현하는건 추후 업데이트 시킬 방법론과 관련이 있다.)

Limitation

위처럼 EDL은 비교적 쉬운 방법으로 model uncertainty를 예측하고 그 뿐 아니라 어떤 model uncertainty인지도 구별할수 있는 장점이 있지만, high data uncertainty를 가지는 data set 즉 높은 aleatroric uncertainty를 가지는 경우에 uncertainty를 상당히 보수적으로 예측하는 단점이 있다. 예컨데 “4”, “9”같은 데이터가 섞여있거나, “1”, “7”과 같은 구별하기 힘든 경우를 생각하면 있다. 그래서 새로이 각 training sample의 class에 중요도에 따라 weight를 부여하는 Fisher Information based Evidential deep Learning이 제안되었다.

2. Fisher Information Evidential Deep Learning($\mathbf{I}$-EDL)

6. 참고자료

1. Van der Maaten, Laurens, and Geoffrey Hinton. "Visualizing data using t-SNE." Journal of machine learning research 9.11 (2008).
2. Hinton, Geoffrey E., and Sam Roweis. "Stochastic neighbor embedding." Advances in neural information processing systems 15 (2002).
3. Wattenberg, et al., "How to Use t-SNE Effectively", Distill, 2016. http://doi.org/10.23915/distill.00002
4. https://scikit-learn.org/stable/modules/generated/sklearn.manifold.TSNE.html

댓글남기기

참고