Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning

목차

• Introduction
• Distribution assumption
• KL-divergence
• Optimization
• Inference
• Summary

제일 처음 공부했던 Bayesian neural network 방법론인 MC-DropOut을 정리해보려 한다. 이 논문의 경우 인용수가 BNN 관련된 paper 중에 가장 많고, 그만큼 리뷰글도 많은데 그럼에도 내가 이해한것을 정리해 보고 싶어 작성한다. 이 글은 원본 논문의 흐름을 따라가지 않고 내 나름의 재구축을해 작성할 것이다.

1. Introduction

불확실성과 관련된 내용은 이전 IEDL에 대해 다룬 글에서 설명하니 생략하도록 하자. 불확실성을 추정하기 위한 방법으로 Bayesian 방법론을 사용하는데, 이번엔 variational inference 방법론을 적용하되 BBP처럼 이 자체를 loss function으로 삼아 SGD를 한것이 아닌 variational distribution을 가우시안이 아닌 특수한 분포로 줌으로써 이것이 Dropout을 통해 구해진 neural network를 통해 근사됨을 보일 것이다. 이런식으로 BBN 모델을 구축하는걸 저자들은 MC-dropout이라 칭하는데, 이것을 통해 inference를 진행할 때 평균으로 예측을 하고, 분산을 통해 모델 불확실성을 추정한다.

또한 편의상 이후 내용에선 한개의 은닉층을 가지는 회귀문제만을 고려할 것이다. 이는 어렵지 않게 다중 은닉층 문제로 확대 가능하며, 단순히 손실함수를 MSE에서 Cross-entropy로 바꾸면 회귀문제를 분류문제로 바꿔 생각가능하다.

2. Distribution assumption

이번 절에서는 각 weight에 주어진 사전분포와 사후분포를 근사하는 variational distribution 그리고 $y \mid x,\omega$ 이 조건부분포를 어떻게 가정할지 생각해 보자.

2.1. Prior distribution

사전분포의 경우 모든 weight이 독립이고 동일하게 $N(0, 1)$을 따른다 가정하자. 이때 문제에 따라 precision $\tau$를 hyperparameter로 취급해 $N(0, \frac{1}{\tau^{2}})$ 을 따른다 가정할 때도 있다. 다만 이 경우 추후 유도의 편의성을 위해 표준정규분포를 따른다 가정할 것이다.

2.2. Conditional distribution of $y$ when $x, \omega$ are given

$\sigma(x)$를 relu function과 같은 활성화함수라 하자. 이때 일반적인 MLP에서 입력값 $x$에 대한 출력값은 $\sigma(x W_{1})W_{2}$ 이 된다. 여기서는 $y \mid x,\omega$ 의 분포가 이를 평균으로 가진다고 가정하자. 즉,

\[y \mid x,\omega \sim N(\sigma(x W_{1})W_{2}, \tau^{-1}I_{D})\]

라 가정하자. (이 때, $y$의 차원이 $D$ 인 경우를 고려한다.)

2.3. Variational distribution

실제 사후분포는

\[p(\omega \mid X, Y) = \frac{p(Y,X \mid \omega)p(\omega)}{p(X,Y)}\]

로 구해지는데 이것의 분모 $p(X,Y) = \int p(X,Y,\omega) d\omega$ 를 실제 closed form으로 구하기 어려운 경우가 많아 이를 직접 구할 수 없어 이를 근사하는 variational distribution을 도입한다.

이전 BBP에서는 이를 정규분포 혹은 정규분포의 혼합분포로 가정하였는데 여기선 그보다 특수한 형태를 가정한다. MC-dropout을 유도하기 위해서 Variational distribution $q_{\theta}(\omega)$을 다음과 같이 가정한다.

\[\begin{align*} W_{1} = diag(z_{1j})M_{1} + \sigma \epsilon_{1} \\ W_{2} = diag(z_{2q})M_{2} + \sigma \epsilon_{2} \end{align*}\]

where, $z_{1j}, z_{2q} \overset{iid}{\sim} bernoulli(p), j = 1,2,\cdots,Q ,\, q = 1,2,\cdots,K$ and each elements of $\epsilon_{1}, \epsilon_{2}$ follow independently and identically $N(0,1)$.

여기서 $Q$는 입력값의 차원이고, $K$는 은닉층의 차원이다. 또한 Variational parameter $\theta$는 $\theta = (M_{1}, M_{2})$로 구성되며 우리의 목적은 특정 loss를 최소화 하는 $\theta$를 구하는 것이다. 저 특정 loss에 대해선 다음 절에서 다루도록 하자.

3. KL-divergence

바로 이전 절에서 언급한 loss function에 대한 이야기를 해보자. 말했듯 Variational distribution은 사후분포를 근사한다. 이때 “근사를 잘 한다”라고 이야기 하기 위해선 어떤 조건을 만족해야 할까?

가장 기본적으로 생각할 수 있는건 두 분포사이의 거리가 가깝다면 “근사를 잘 한다.” 라고 말 할 수 있을 것이다. 그렇다면 통계적으로 “두 분포사이의 거리”를 어떻게 정의 해줘야 할까? 이것에는 Total variation, $\chi^{2}$ divergence 등 여러 가지 측도가 있지만 여기서는 KL-divergence를 사용한다. 여기서 한가지 주의해줘야 할 점은 거리를 나타내기 위해 KL-divergence를 사용한다 했지만 이것이 수학에서 정의하는 “Metric”이 되지는 않는다. 두 분포 $P, Q$ 사이의 KL-divergence는 다음과 같이 정의한다.

\[KL(P, Q):= \begin{cases}\int \log \frac{d P}{d Q} d P & \text { if } P \ll Q \\ +\infty & \text { otherwise. }\end{cases}\]

여기서 $P \ll Q$는 각각의 확률밀도함수 $p,q$에 대해서 $p>0 \Rightarrow q>0$임을 의미한다.

해당 식에서 볼 수 있듯, $K(P, Q) \neq K(Q, P)$이므로 symmetric하지 않아 metric이 되지 않는다.

3.1. Variational approximation

KL-divergence를 적용해 사후분포 $p(\omega \mid X,Y)$와 Variational distribution $q_{\theta}(\omega)$ 사이의 거리를 측정한것은 다음과 같이 쓸 수 있다.

\[\begin{align*} &KL(q_{\theta}(\omega), p(\omega | X, Y)) = \\ & \int q_{\theta}(\omega) \log \frac{q_{\theta}(\omega)}{p(\omega | X, Y)} d \omega \end{align*}\]

또한 추가적인 계산을 통해 다음과 같은 형태로 표현 가능하다.

\[\begin{align} &KL(q_{\theta}(\omega), p(\omega | X, Y)) = \nonumber \\ &- \int \log f(Y | X, \omega) q_{\theta}(\omega) d \omega + KL(q_{\theta}(\omega), p(\omega)) + Constant \end{align}\]

EM-알고리즘이나, 생성모델을 다루는 분야에서는 위 식에 -1을 곱한 값을 Evidence of Lower Bound(ELBO)라 부른다. 이는 $p(Y) \geq \text{ELBO}$ 로 쓸수 있다. 즉 ELBO 값이 커지면 커질 수록 관측값의 Evidence 가 높아져 더 좋은 모델이 된다는 의미로 해석 가능하다. 여기서 ELBO 값이 커진단건 우리의 KL-divegece는 더 작아진단 걸로 이해할 수 있을 것이다. 이 내용은 여기까지만 하고 더 자세한건 추후 Diffusion과 같은 생성모델을 다룰 기회가 있다면 그때 다루도록 하겠다.

3.2. Interpretation of KL-divergence

(1) 식에 대해서 보충설명을 하고 싶다. 위에서 언급했듯 결국 우리의 목표는 거리를 좁하는것이고 KL-divergece를 작게 할수록 evidence가 더 커져 좋은 모델이 된다고 하였다. 그렇다면 (1)을 작게한다는 것이 어떤 의미를 가지고 있을까? 이는 두가지 파트로 나눠서 생각 가능하다.

1. Likelihood term: $- \int \log f(Y

   X, \omega) q_{\theta}(\omega) d \omega$ 이 파트를 의미한다. 여기서 $\int \log f(Y

   X, \omega) q_{\theta}(\omega) d \omega$ 를 크게 해 줘야 KL-divergence는 작아지므로 결과적으로 모델 복잡도를 늘려 가능도를 높혀주는 항으로 이해 가능하다. 즉 일반적인 머신러닝 모형에서 MSE나 Cross-entropy에 해당하는 항이다.

2. KL-divergece term: $KL(q_{\theta}(\omega), p(\omega))$이 KL-divergec로 계산되는 항을 의미한다. 전체값을 작게 해주기 위해선 Likelihood term과 반대로 이를 작게 해줘야 하는데 이럴시 Variational distribution과 사전분포 사이의 거리를 가깝게 하도록 한단걸 의미한다. 이때 사전분포를 간단한 정규분포 등으로 가정하는걸 고려하면 Variational distribution가 너무 복잡해주지 않도록 규제해주는 역할을 한다. 그래서 이 항을 Regularization term로도 부른다. 일반적인 머신러닝에서는 $L_{2}$ Regularization에 해당하는 항이다.

4. Optimization

우리의 목표는 이제

\[\begin{align} \argmin_{\theta} - \int \log f(Y | X, \omega) q_{\theta}(\omega) d \omega + KL(q_{\theta}(\omega), p(\omega)) \end{align}\]

인 Variational parameter인 $\theta$를 찾는 것인데, 실제 이것을 바로 계산하기엔 어려움이 따른다. 그래서 몇 가지 근사와 계산을 통해 (2)식을 변형하고 그것을 최소로 하는 $\theta$가 어떻게 Dropout으로 구해진 weight와 동할한지 알아보도록 하자.

4.1. Monte Calro Approximation

먼저 $\int \log f(Y

X, \omega) q_{\theta}(\omega) d \omega$ 이 항에 대해서 생각해보자. 실제 저 식들은 알고있지만 문제는 저걸 closed form으로 계산하고 적분하는게 사실상 불가능에 가깝다. 그래서 이걸 실제 수학적으로 푸는게 아닌 Monte Calro 적용해 $q_{\theta}(\omega)$ 에서 표본추출해 계산한다. 일단 각 데이터셋이 모두 독립이므로 이는 다음과 같다.

\[\int \log f(Y | X, \omega) q_{\theta}(\omega) d \omega = \sum_{i = 1}^{N} \int \log f(y_{i} \mid x_{i}, \omega) q_{\theta}(\omega) d \omega\]

이제 $\int \log f(y_{i} \mid x_{i}, \omega) q_{\theta}(\omega) d \omega$ 를 근사하기 위해 Monte Calro를 사용한다. 다만 이 논문에서 제일 이해가 되지 않는 부분 중 한 곳이 여기인데 보통 Monte Calro를 사용한다하면 분포로 부터 여려개의 표본을 추출해 그것의 표본평균으로 적분(모평균)을 근사하는데 이 경우 각각의 인덱스 $i$에 대하여 “하나의” 표본만 추출해 적분을 근사했다. 그래서 위 식을 다음과 같이 근사한다.

\[\begin{align} \int \log f(Y | X, \omega) q_{\theta}(\omega) d \omega &= \sum_{i = 1}^{N} \int \log f(y_{i} \mid x_{i}, \omega) q_{\theta}(\omega) d \omega \\ &\approx \sum_{i = 1}^{N} \log f(y_{i} \mid x_{i}, \omega_{i}) \text{ where } \omega_{i} \sim q_{\theta}(\omega) \end{align}\]

위에서도 언급했듯 내 생각에는 (4)에서 보다 정확히 근사하기 위해선 합의 합꼴로 나태내져야 맞다 생각하는데 여기선 이미 합형태이고 각 index에서 각각이 $\omega_{i}$를 추출해 그것의 합을 구하는 것이니 충분하다 생각했는지 하나의 표본만 추출해 의아함이 남는다.

여하튼 여기서 만약 우리가 가정한것처럼 회귀문제이면 저 log-likelyhood는 $-MSE$와 비례할 것이고 그렇지 않고 분류문제이면 $-CE$와 비례할 것이다. 그래서 이 식을 (2)에 대입한다면 DNN에서 loss function의 형태가 나오게 된다.

4.2. More Calculation

이 파트는 (2)식에서 $KL(q_{\theta}(\omega), p(\omega))$ 이것을 계산하고 근사해 변형하는 것에 대해서 다룬다.

다만 이 과정이 길고 지루하며 통계적 계산능력을 요구하기 때문에 여기선 자세히 다루진 않고 결과만 쓰도록 하자. 만약 궁금한 사람이 있다면, (Gal, 2016)의 Appendix를 참고하자.

$KL(q_{\theta}(\omega), p(\omega))$은 다음과 같이 근사할 수 있다.

\[\begin{align} KL(q_{\theta}(\omega), p(\omega)) \approx \frac{p}{2} ||M_{1}||^{2} + \frac{p}{2} ||M_{2}||^{2} + Constant \end{align}\]

4.3. Relationship with Dropout

(2),(4),(5)를 종합하면 결과적으로 우리가 구해야하는 값은 다음과 같다.

\[\argmin_{\theta} \frac{\tau}{2} \sum_{i=1}^{N} ||y_{i} - \sigma(x_{i}W_{i1})W_{i2}||^{2} + \frac{p}{2} ||M_{1}||^{2} + \frac{p}{2} ||M_{2}||^{2} \text{ where } \omega_{i} \sim q_{\theta}(\omega)\]

이 때 나누는 것은 최소가 되는 $\theta$를 구하는 것에 영향을 주지 않으므로 최적화 식을 $\frac{\tau}{2}$로 나누고, $\lambda = \frac{p}{\tau}$로 설정한 뒤 $W$안에 숨어 있는 $\sigma$를 0으로 극한을 보내면 다음 식을 얻을 수 있다.

\(\begin{align} \argmin_{M_{1},M_{2}}\sum_{i=1}^{N} ||y_{i} - \sigma(x_{i}diag(z_{i1j})M_{1} )diag(z_{i2q})M_{2} ||^{2} + \lambda ||M_{1}||^{2} + \lambda ||M_{2}||^{2} \end{align}\) where, $z_{i1j}, z_{i2q} \overset{iid}{\sim} bernoulli(p), j = 1,2,\cdots,Q ,\, q = 1,2,\cdots,K$.

이 식을 만족하는 $M_{1},M_{2}$는 DNN에서 Dropout을 사용해 얻어진 weight와 정확히 동일한 식이므로 해당 weight를 사용해 Variational parameter를 근사가능하다.

5. Inference

4장 까지의 내용을 통해 weight의 사후분포를 근사하는 Variational distribution을 Dropout DNN을 통해 구할 수 있단 걸 구했다. 그렇다면 이것을 어떻게 해야 Bayesian으로 해석 가능할까. 일반적인 Dropout DNN과의 차이는 과연 무엇일까? 그것은 바로 Inference 과정에서 발생한다. Training 시에는 똑같이 진행되지만 Dropout DNN에서는 inference 할 때 Dropout을 적용시키지 않고 한개의 고정된 출력값을 구하는 반면, MC-Dropout에서는 inference시에도 Dropout을 적용한다. 그에 따라 한개의 입력값에 대해 여러 출력값이 나올 수 있다.

쉽게 설명해 MC-Dropout은 한개의 입력값 $x$에 대해 inference를 진행할 때 Dropout을 적용한 여러번의 반복을 통해 여러 출력값 $y_{t}$를 얻고 이것의 평균으로 예측값을 얻어내고, 분산으로 모델 불확실성을 추정한다. 직관적으로 다음 그림을 참고하면 좋을 것 같다.

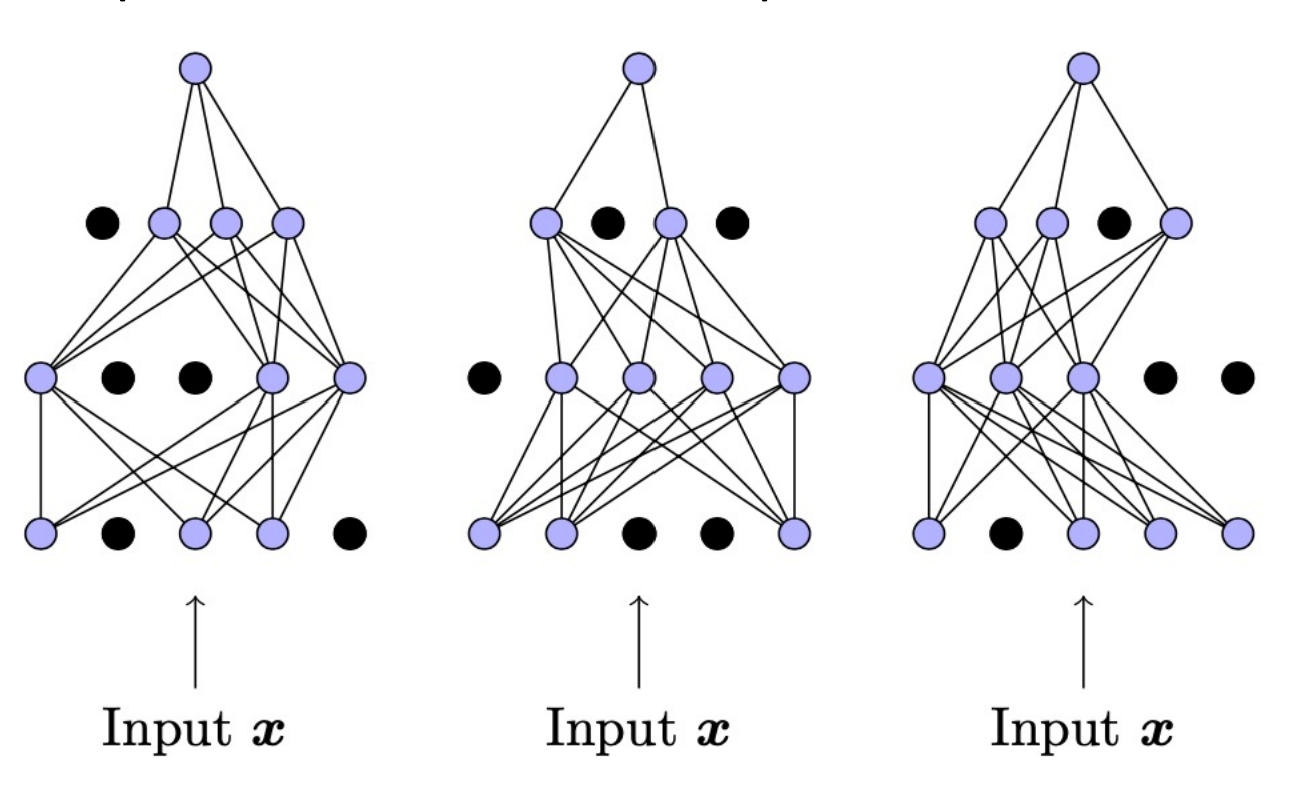
다시 말해 $y \mid x$의 분포에서 표본추출하는 과정을 반복하는 것이다. 그리고 그 표본들을 이용해 분포의 통계량들을 추정할 수 있다. 저 표본들의 표본평균과 표본 분산이 실제 평균, 분산의 불편추정량으로 근사할 수 있다는걸 이론적으로 증명할 수 있으나 해당 포스팅의 범위를 넘는다 판단해 여기에 담지 않도록 하겠다. 관심있는 독자들은 (Gal, 2016)의 Appendix를 참고하자.

6. Summary

지금까지 MC-Dropout에 대해 정리해봤다. 사실 해당 논문에는 이 내용 의외에도 BNN이 Deep-GP로 수렴한다는 내용을 다뤄 보다 어렵지만, 내 생각에 그건 당장에 필요한 부분은 아닌 것 같아 굳이 다루지 아니 하였다. 의미있는 내용이지만 굳이 같은 논문에서 다룰만큼 잘 어우러지냐? 라고 하면 사실 나는 잘 모르겠더라. 처음 Bayesian neural network를 공부하려 했을때 “처음 공부하는 것이니 인용수가 제일 높은거 부터 읽어보자” 라고 생각해 읽게된 논문이다. 이때만 해도 논문 읽는게 익숙하던 때가 아니었어서 처음 읽을때 엄청 어렵고 해맸던 기억이 나는데 그게 벌써 1년하고도 6개월 전이다. 막상 나중에 선배한테 물어보니 다른 방법론들에 비해 성능이 안좋기 때문에 그렇게 많이 안 쓴다고 한다. 근데 왜 인용수가 높냐고 물어보니 성능이 안좋아 baseline으로 쓰기 좋기때문에 이곳 저곳에 많이 불려나가서 그렇다는데…. 그럼에도 한 번쯤은 정리 해둘 필요가 있을 것 같아 대략적인 내용은 정리 한 것 같다.

7. Reference

1. Gal, Yarin, and Zoubin Ghahramani. "Dropout as a bayesian approximation: Representing model uncertainty in deep learning." international conference on machine learning. PMLR, 2016.