논문리뷰: Bayesian Learning via Stochastic Gradient Langevin Dynamics

2024-01-24

1. Introduction

Bayesian learning을 하는데 있어서 가장 문제가 되는 것은 사후분포(posterior distribution)가 closed form이나 잘 알려진 형태로 구해지지 않아서 다루기 어렵다는 것이다. 이를 다루기 위한 한가지 방법으로 사후분포에서 표본(sample)을 추출해 이것의 표본 통계량으로 사후분포의 통계량을 근사하는 것이다 (Strong Law of Large Number). 하지만 여기서 사후분포의 차원이 일차원이 아닌 다차원인 경우에 사후분포로부터 독립인 표본을 추출하는 것이 어려워, markov chain인 표본을 추출해 이를 통해 사후분포를 근사한다 (Ergodicity).

가장 잘 알려진 MCMC 방법론으로는 깁스 추출법(Gibbs sampling)과 해밀턴 몬테 카를로(Hamiltonian Monte Carlo)가 있다. 다만 이러한 방법들의 경우 데이터 셋이 커질시 계산시간이 오래걸리는 것이 알려져있다.

여기서는 큰 데이터 셋에 적합하기 위한 scalable한 방법론을 제시하기 위해 해밀턴 몬테 카를로의 변형인 랑게빈 몬테 카를로 (Langevin Monte Carlo)와 확률적 경사 하강법(Stochastic Gradient Descent)을 결합한다.

2. Preliminaries

이번 챕터에서는 본격적인 논의에 들어가기 앞서 사전지식들에 대해 간단하게 알아보도록 하자.

기본적인 가설로 $\theta$ 를 사전분포 $p(\theta)$ 를 따르는 모수라 하고, $p(x \mid \theta)$ 를 $\theta$ 가 주어졌을 때 $x$ 의 조건부 분포라 하자. 그리고 $N$ 개의 데이터 $X = [ x_{i} ]_{i=1}^{N}$ 이 관측되었다고 하자. 이 때 사후분포는

\[\begin{align} p(\theta | X) \propto p(\theta) \prod_{i=1}^{N} p(x_{i}| \theta) \end{align}\]

로 구해진다. 또한 곱 보다는 합을 다루는게 쉬우므로 여기에 로그를 취한

\[\begin{align} \log p(\theta | X) \propto \log p(\theta) + \sum_{i=1}^{N} \log p(x_{i}| \theta) \end{align}\]

를 많이 사용한다.

보통의 머신러닝이나 답러닝의 경우 (2) 을 최대로 하는 “Maximum a posterior” (MAP)를 구해 $\theta$를 추정하고, bayesian learning에서는 저 분포로 부터 표본을 추출해 사후분포를 추정한다.

확률적 경사 하강법 (Stochastic Gradient Descent)

경사 하강법(Gradient Descent)은 MAP나 MLE(Maximum Likelyhood Estimator) 즉 특정식에서 최댓값(최솟값)을 구하는 알고리즘이다. 이를 큰 데이터셋에 더 효율적으로 적용하기 위해서 각 반복시에 데이터 셋을 랜덤하게 mini-batch 단위로 나눠 그것만으로 각 시행에서 update 하는것을 확률적 경사 하강법(SGD)라고 한다. 이는 보통의 경우 최적화에서 가장 많이 사용되는 알고리즘이다. 각 반복 $t$ 마다 업데이트 되는 $\theta$값은 다음과 같다.

\[\begin{align} \Delta \theta_t=\frac{\epsilon_t}{2}\left(\nabla \log p\left(\theta_t\right)+\frac{N}{n} \sum_{i=1}^n \nabla \log p\left(x_{t i} \mid \theta_t\right)\right) \end{align}\]

이 때, local maximum으로 잘 수렴하기 위해서는 step size $\epsilon_t$가 다음 조건을 만족해야 함이 알려져 있다.

\[\begin{align} \sum_{t=1}^{\infty} \epsilon_t=\infty \quad \sum_{t=1}^{\infty} \epsilon_t^2<\infty \end{align}\]

다만 이렇게 구한 MAP, MLE 추정량은 불확실성(uncertainty)를 추정하기 어렵고, overfitting의 가능성이 있다는 단점이 있다.

랑게빈 몬테 카를로 (Langevin Monte Carlo)

(1)로부터 샘플을 추출하는 방법 중 한개로 Langevin 동역학으로 부터 아이디어를 얻은 랑게빈 몬테 카를로가 있다. 이는 해밀턴 몬테 카를로를 변형한 방법으로 $\theta$를 다음과 같이 업데이트 해 마코프 체인을 얻는다.

\[\begin{align} \Delta \theta_t & =\frac{\epsilon}{2}\left(\nabla \log p\left(\theta_t\right)+\sum_{i=1}^N \nabla \log p\left(x_i \mid \theta_t\right)\right)+\eta_t \nonumber \\ \eta_t & \sim N(0, \epsilon I) \end{align}\]

이로부터 $\theta * = \theta_{t} + \Delta \theta_t$ 로 한뒤 메트로폴리스-헤이스팅스(Metropolis-Hastings) 알고리즘을 적용해 합격하면 $\theta_{t+1} = \theta *$ 그렇지 않으면 $\theta_{t+1} = \theta_{t}$로 업데이트한다.

여기서 확인해야 할 점은, gradient term 앞에 붙은 $\epsilon$과 뒤에 더해진 노이즈의 분산이 동일해야 한다는 점이다.

3. Stochastic Gradient Langevin Dynamics

확률적 경사 하강법 (3)과 랑게빈 몬테 카를로 (5)를 비교하면 상당히 유사함을 알 수 있다. 이를 통해 이 두 방법론을 함께 고려하려는 시도는 자연스러운 생각이다. 그러한 방법을 Stochastic Gradient Langevin Dynamics이라 한다. 큰 데이터 셋에 대해서 효율적으로 MCMC를 진행하는 방법으로 볼 수 있다. 그 식은 다음과 같다.

\[\begin{align} \Delta \theta_t & =\frac{\epsilon_t}{2}\left(\nabla \log p\left(\theta_t\right)+\frac{N}{n} \sum_{t=1}^n \nabla \log p\left(x_{t i} \mid \theta_t\right)\right)+\eta_t \nonumber \\ \eta_t & \sim N\left(0, \epsilon_t\right) \end{align}\]

이 때 step size $\epsilon_{t}$는 SGD와 마찬가지로 (4)의 조건을 만족해야 $\theta_{t}$의 chain이 사후분포로 잘 수렴한다. (6)의 식을 보면 SGD의 식 (3)에 랑게빈 랑게빈 몬테 카를로 처럼 정규분포를 따르는 노이즈를 더해준 꼴로 이해할 수있다. 이때 노이즈가 없다면 $\theta_{t}$가 local maximum으로 수렴하지만 저런식으로 노이즈를 더해주면 그것의 chain이 사후분포를 수렴하다난 것에 의의가 있다.

또한 이때 $t$가 커짐에 따라 $\epsilon_{t} \rightarrow 0$이기 때문에 합격확률이 1로 수렴하게 되서 일반적인 랑게빈 몬테 카를로와 다르게 메트로폴리스-헤이스팅스 단계가 필요하지 않다는 장점이 있다.

4. Example

간단한 상황에서 SGLD를 직접 구현해 보고 실제 잘 작동하는지 확인해 보자.

Beta prior

가장 간단한 상황으로 $\theta \sim Beta(5,5)$이고 $x \mid \theta \sim bernoulli(\theta)$ 인 경우를 고려해보자. 이로부터 데이터 $X$ 가 관측되었다면 $\theta$ 의 사후분포는 $\theta \mid X \sim Beta(5 + \sum_{i=1}^{N} x_{i} , N + 5 - \sum_{i=1}^{N} x_{i} )$ 임은 쉽게 계산할 수 있다. 본래라면 사후분포를 closed form으로 계산할 수 있기 때문에 굳이 MCMC를 사용할 필요는 없지만 이 경우에는 실제 SGLD를 통해 추출한 표본들이 사후분포로 잘 수렴하는지를 확인해보기 위해서 해당 상황으로 세팅을 했다.

또한 시뮬레이션 상황에서 $\theta$의 사전평균이 $\frac{1}{2}$이므로 $x \sim bernoulli(\frac{1}{2})$로 부터 추출하였다.

# import the module
import numpy as onp
import jax.numpy as np
import jax.scipy as sp
from jax import grad, jit
from tqdm import tqdm
from matplotlib import pyplot as plt

# Define the data generating function.
def gen_data(n=100):
    x = onp.random.choice([0,1], size = n, p =[1/2,1/2])
    return x

# Define the log likelihood and log prior.
def log_prob_prior(theta, a = 5, b= 5):
    return sp.stats.beta.logpdf(theta[0], a,b)
def log_prob_lik(theta, x):
    likelyhood = sp.stats.bernoulli.pmf(x, theta[0])
    return np.mean(np.log(likelyhood))

# Defien the epochs and generate the data.
epochs = 100
x = gen_data()

# Get the gradient of log likelihood and log prior.
log_prob_prior_g = jit(grad(log_prob_prior))
log_prob_lik_g = jit(grad(log_prob_lik))

# Initial value and empty vector to save chian of theta.
theta = onp.random.uniform(0,1,1)
thetas = onp.zeros((epochs * len(x), 1))  

a =1
b=100000000

# Iterate
for i in tqdm(range(epochs * len(x))):
    eps = a * (b+i) **(-0.55)    # step size
    noise = onp.random.randn(1) * np.sqrt(eps)    # noise eta_{t}   
    idx = i % len(x)    # Index, In this case we let batch size as n=1.
    grad =  log_prob_prior_g(theta)  + len(x) * log_prob_lik_g(theta, x[idx])
    theta = theta + 0.5 * eps * grad + noise    # Update the theta
    thetas[i] = theta    # Save the theta


# Plot the posterior distribution and histogram of sample
plt.hist(thetas, bins=100,density=True)
x_values = np.linspace(0, 1, 1000)
pdf_values = sp.stats.beta.pdf(x_values,5 + np.sum(x), 5 + len(x) - np.sum(x))
plt.plot(x_values, pdf_values, label=f'Beta({5}, {5})')
plt.show()

png

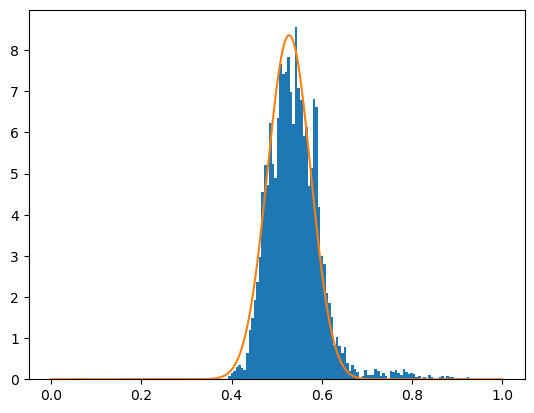
사후분포의 plot과 표본들의 histrogram을 비교해봤을 때 표본들이 얼추 사후분포로 잘 수렴함을 확인가능했다. 실제 사후분포를 closed form으로 구할 수 없는 경우 이런 방법으로 뽑은 표본들을 통해 사후분포들의 여러 통계량(평균, 중앙값, 분위수 등)을 계산해 베이즈 추정을 진행할 수 있다.

Bivariate normal distribution

이번에는 위에 보단 조금 복잡한 예시로 실제 사후분포를 구하기 어렵고 $\theta$의 차원이 이차원인 경우에 대해서 고려해 보자. $\theta = (\theta_{0}, \theta_{1})$이고 $\theta_{0} \sim N(0, 10)$, $\theta_{1} \sim N(0,1)$이고 각각이 독립인 사전분포를 따른다 하자. 또한 $\theta$가 주어졌을때 데이터 $x$의 분포는 $x \mid \theta \sim \frac{1}{2} N(\theta_{0},2) + \frac{1}{2} N(\theta_{0} + \theta_{1},2)$인 mixture normal distribution으로 주어진다 하자.

이 경우는 위와 달리 실제 사후분포를 closed form으로 구하기 어려워 실제 추정시 사후분포로부터 표본을 추출해 추정을 진행한다. Sample code는 위의 경우와 크게 다르지 않음을 확인할 수 있다.

# import the module
import numpy as onp
import jax.numpy as np
import jax.scipy as sp
from jax import grad, jit
from tqdm import tqdm
from matplotlib import pyplot as plt

# Define the data generating function.
def gen_data(n=100):
    x = 0.5 * np.sqrt(2) * onp.random.randn(n) + \
        0.5 * (np.sqrt(2) * onp.random.randn(n) + 1)
    return x

# Get the gradient of log likelihood and log prior.
def log_prob_prior(theta, sigma_1=np.sqrt(10), sigma_2=1):
    return sp.stats.norm.logpdf(theta[0], loc=0, scale=sigma_1) + \
           sp.stats.norm.logpdf(theta[1], loc=0, scale=sigma_2)
def log_prob_lik(theta, x):
    log_lik = 0.5 * sp.stats.norm.pdf(x, loc=theta[0], scale=np.sqrt(2)) + \
              0.5 * sp.stats.norm.pdf(x, loc=np.sum(theta), scale=np.sqrt(2))
    return np.mean(np.log(log_lik))

# Defien the epochs and generate the data.
epochs = 10000
x = gen_data()

# Get the gradient of log likelihood and log prior.
log_prob_prior_g = jit(grad(log_prob_prior))
log_prob_lik_g = jit(grad(log_prob_lik))

# Initial value and empty vector to save chian of theta.
theta = np.zeros(2)
thetas = onp.zeros((epochs * len(x), 2))

b = 1 / ((1 / (onp.exp(-onp.log(100) / 0.55)) - 1) / (epochs * len(x)))
a = 0.01 / b ** (-0.55)

# Iterate
for i in tqdm(range(epochs * len(x))):

    eps = a * (b + i) ** (-0.55)    # step size
    noise = onp.random.randn(2) * np.sqrt(eps)    # noise eta_{t}   
    idx = i % len(x)    # Index, In this case we let batch size as n=1.
    grad = log_prob_prior_g(theta) + len(x) * log_prob_lik_g(theta, x[idx])
    theta = theta + (0.5 * eps * grad + noise)   # Update the theate
    thetas[i] = theta    # Save the theta

# Plot the 2D histogram of sample of posterior.
plt.hist2d(thetas[:, 0], thetas[:, 1], bins=100)
plt.show()

png

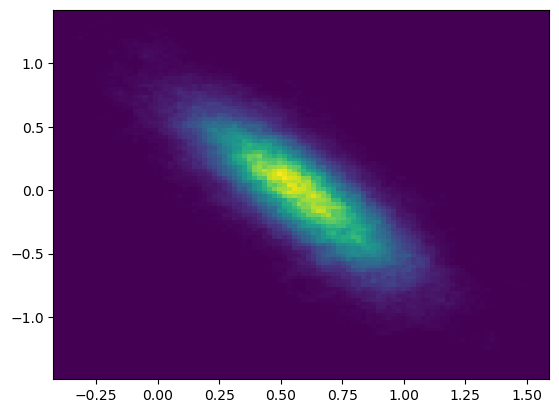
사후분포를 추정해서 그린 그래프는 위와 같고, 밝은 부분에서의 확률값이 크다고 해석할 수 있다. 이를 통해서 $\theta_{0}$와 $\theta_{1}$이 음의 상관관계를 가지고 대략 각각이 0.6, 0일 때의 확률이 가장 큼을 확인 가능하다. 이렇게 $\theta$의 분포를 보면 그것의 분산을 알 수 있고 이를 통해서 일반적인 SGD에서는 할 수 없는 불확실성 추정을 할 수 있다.

5. Summary

확률적 경사 하강법은 예측이란 관점에서는 좋은 알고리즘이지만 이를 사용할 시에 과적합의 가능성이 있고 불확실성을 측정할 수 없다는 단점이 있다. 마르코프 체인 몬테 카를로는 사후분포로부터 표본을 추출해 사후분포를 근사함으로써 과적합에 대한 내성이 있고 불확실성을 측정할 수 있다는 장점이 있지만, 추정시 모든 데이터를 계산해야 하므로 계산시간이 오래걸린다는 단점이 있다.

여기서는 두 방법을 보완한 방법인 Stochastic Gradient Langevin Dynamics으로 간단하게 확률적 경사 하강법에 normal noise를 섞어줌으로써 사후분포를 근사하는 chian을 얻을수 있음을 보였다. 이 방법을 통해서 지금까지 비효율적이었던 큰 데이터 셋에서의 사후분포 추정을 보다 효율적으로 할 수 있다.

6. Reference

1. Welling, M., & Teh, Y. W. (2011). Bayesian learning via stochastic gradient Langevin dynamics. In Proceedings of the 28th international conference on machine learning (ICML-11) (pp. 681-688).
2. https://gist.github.com/tonyduan/9cc2d8f4412635a37e0ac13c793409e2

Twitter Facebook LinkedIn

논문리뷰: Bayesian Learning via Stochastic Gradient Langevin Dynamics

목차

1. Introduction

2. Preliminaries

확률적 경사 하강법 (Stochastic Gradient Descent)

랑게빈 몬테 카를로 (Langevin Monte Carlo)

3. Stochastic Gradient Langevin Dynamics

4. Example

Beta prior

Bivariate normal distribution

5. Summary

6. Reference

공유하기

댓글남기기

참고

CYCLICAL STOCHASTIC GRADIENT MCMC FOR BAYESIAN DEEP LEARNING

Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning

Laplace Approximation for neural networks

논문리뷰: Weight Uncertainty in Neural Networks