논문리뷰: What Are Bayesian Neural Network Posteriors Really Like - 1?
목차
- Introduction
- Background
- Related work
- HMC for deep neural network
- Reference
원래는 논문을 읽고 포스팅으로 정리하는 편인데 이번에는 한번 읽으면서 정리하면 어떨까 싶다. 해당 논문이 워낙 길기도 하고 방법론을 제시하기보단 BNN의 성질들에 대해 살펴보는 형식의 논문이다 보니 핵심적인 방법론만 딱! 하고 정리하기도 어렵다 생각해 해당 방식으로 작성해보려 한다.
이 포스팅은 ICML 2021에 accept된 “What Are Bayesian Neural Network Posteriors Really Like?”라는 논문이다. 뉴욕대와 구글 ai researcher팀이 한 공동연구로 Abstract만 읽어봐도 보통은 잘 진행하지 않을? 어찌보면 기행?으로 BNN의 성질을 밝히려 시도한다.
보통 BNN의 경우 weight의 사후분포를 closed form으로 구하기 어렵고 이게 다루기가 어렵기 때문에 Variational inference나 MCMC 등을 사용해 사후분포를 근사시킨다. 이때 MCMC를 사용한다하면 이 경우에 사후분포로부터 표본추출을 해야하기 때문에 계산량이 많아 보통의 경우 SGMCMC(SGLD 등, 참고:https://yunseopshin.github.io/deep_learning/SGLD/)을 많이 사용하고 보통 epochs 수 또한 1~5천번 사이인데 이 논문의 경우 확장가능성과 실용가능성은 고려하지 않고 full batch HMC를 사용하고 epochs 수 또한 6천만(,,,,,) epochs으로 시행했다고 한다. 그러기 위해서 512개의 TPU를 사용해서 병렬처리를 했다고 하는데 정말 대단한거 같다…
1. Introduction
Deep neural network에서 bayesian inference를 사용하는 것은 prediction, uncertainty, model comparison, active learing, continual learning, decision making 등에 이점을 준다. 또한 Bayesain comunity는 astrophysics, automatic diagonis, advertising model, fluid dynamics model 등 다양한 분야에서 각광을 보여왔다. 즉 간단하게 말해서 BNN은 여러가지 장점들을 가지고 있으며 여런 분야에서 성공적으로 적용됐다.
하지만 최근의 neural network는 weight의 수가 기하급수적으로 늘어나고 사후분포가 unimodal이 아닌 multi modal의 형태이기 때문에 이를 다루기 어렵고 그러기 위한 컴퓨팅 제약도 늘어났다.
이런 문제를 다루기 위해 여러 방법론이 제시되어왔다.
- Variational inference: Multi modal 사후분포를 간단한 unimodal gaussian 분포로 근사함.
- Deep ensemble: Bayesian inference에서 가장 자연스러운 아이디어이지만, 오직 사후분포의 mode만 표현가능하단 단점이 있음.
- Stochastic MCMC: 컴퓨팅 계산 시간 측면서 이점이 있지만, 사후분포의 평균에 편향되는 추정값을 내는 경향이 있음
- Cold posterior: posterior 분포를 아래의 형태로 계산. 이때 $T «1$일때 좋은 성능을 보임이 알려져 있음. (Aitchiso, 2020)
해당 논문은 full-batch HMC를 사용해 BNN의 사후분포로부터 표본을 추출하는데 위에서도 언급했듯이 이는 BNN의 여러 성질들을 탐구하기 위해서이지 이게 효율적인 방법이여서가 아님을 되새기고 가자.
저자들이 탐구하려고하는 BNN의 성질들은 다음과 같다.
- BNN이 다른 기본적인 모델학습과 ensemble 학습에 비해 performance측면서 상당한 이점이 있다.
- 하나의 긴 HMC chian은 사후분포에 대한 좋은 근사를 제시한다.
- 사후분포 “tempering”은 최적의 예측을 하는데 있어 거의 역할을 하지 못한다. 다만 data argumentation과 함께 이뤄졌을때 performance 향상을 보인다.
- BMA performance는 사전분포 선택에 대해서 robust하다.
- BNN은 convariate shift에 대해서 robust하진 않다.
- SGMCMC가 사후분포에 대한 좋은 근사를 제공하긴 해도, 그것들은 HMC와는 상당히 다른 분포를 제시한다.
저자들은 HNC를 CIFAR-10이나 UCI dataset등 공용 리소스 데이터에 적용시켜 해당 내용들을 보였다.
2. Background
전통적인 학습의 목표는 간단히 말해서 MLE를 최대로 하는 모수를 최적화하는 것이었다. 반면 베이지안 프레임워크안에서는 모수 자체에 분포를 부여해 그것의 사후분포인 $p(\omega \mid \mathcal{D})$를 추론하는게 목적이 된다. 이는 베이즈 정리를 사용해서 구할수 있고 이때, 새로운 데이터 $x$에 대한 inference는 다음과 같은 예측분포를 통해 이뤄진다. \(\begin{align} p(y \mid x, \mathcal) = \int p(y \mid x, \omega)p(\omega \mid \mathcal{D}) d \omega \end{align}\) 여기서 문제점은 사후분포 $p(\omega \mid \mathcal{D})$이게 닫힌형태로 구해지지 않고 다루기가 힘들다는 것이다. 그래서 주로 이를 근사하는 분포를 고려하거나, 이로부터 표본을 추출해 예측분포를 추정한다.
$p(\omega \mid \mathcal{D})$에서 $\omega$의 차원이 커질때 표본추출하는 방법이 Markov chain Monte Calro이다. 여기서는 이를 위핸 방법으로 해밀토니안 몬테 카를로를 사용해 $p(\omega \mid \mathcal{D})$로부터 표본을 추출한다.
3. Related work
해당 챕터에서는 거의 intro에서 했던말을 다시하면서 해당 연구의 중요성을 강조한다.
대부분의 bayesian deep learning은 사후분포를 근사하는 scalable한 방법론에 초점이 맞춰져있었다하며, 이러한 연구들이 정작 실제 데이터에서 true 사후분포와 근사된 사후분포가 얼마나 차이가 있는지 대해서는 다루지 않았다고 비판한다. 또한 표본추출 방법을 다루는 연구들은 대부분 stochastic한 방법위주로 연구되었다고 하며 이러한 방법들은 다음과 같은 이유 때문에 근본적인 편향이 생길수 밖에 없다고 한다.
- 메트로폴리스-헤이스팅스 단계(accept-reject)을 진행하지 않음.
- 전체집단으로부터 batch를 sampling하므로 노이즈가 생길수 밖에 없음.
이러한 이유에서 data subsampling은 본질적으로 HMC와 양립할수 없다는 의견을 보인다. 그뿐 아니라 기존에는 HMC과정에서 leap frog(등넘기)단계시에 $L=100$과 같이 적은 횟수의 반복을 진행하였다면 저자들은 연구를 진행하는데 있어 정확도를 키우기 위해 $L=10^5$과 같은 상황에서 한 epochs을 진행했다고 한다.
이런 방법들이 실제로는 적용이 어렵고 scalable하지는 않지만, 이를 통해 위에서 언급한 BNN의 여러가지 성질들에 탐구할수 있다고 재차 강조한다.
4. HMC for deep neural network
해당 챕터에서는 저자들이 HMC를 적용하는데 있어서 구체적인 실험상황 세팅(데이터, 모델 구조, 하이퍼파라메터, 설험구현법 등)을 설명한다. 먼저 실험구현의 경우 512개의 TPU를 사용해서 병렬처리했다고 하는데 이 내용의 경우 내 관심분야는 아니므로 과감히 스킵하도록 하자.
Neural network model architecture의 경우 “ResNet-20-FRN”와 “CNN-LSTM”을 사용했고 여기서 특이사항은 ResNet에서 활성화함수로 ReLU가 아닌 SiLU(Swish activation)을 사용했다고 하는데 이 이유는 ReLU는 x=0에서 smooth하지 않기때문에 smooth한 사후분포를 얻기 위해서 해당 활성함수를 사용했고 전체 수행능력에 있어서도 ReLU과 큰차이가 나지 않았다고 한다. 데이터셋은 이미지 분류 task에선 CIFAR에 ResNet을 사용했고, 감정분석에 있어서는 IMDB에 CNN을 적용시켰다고 한다. 또한 data argumentation은 그것이 내포한 확률성때문에 사용하지 않았다. 다음으로는 HMC 알고리즘을 적용하는데 있어 사용되는 hyperparameter들에 대해서 알아보도록 하자.
4.1. Trajectory lenght $\tau$.
말이 어려울수 있는데 간단히 말해서 HMC과정중 leap frog 알고리즘을 시행하는 횟수와 관련된 하이퍼파라미터이다. leap frog 알고리즘 반복횟수 $L = \frac{\tau}{\Delta}$로 정의한다고 보면될것같다. (이때 $\Delta$는 후술하겠지만 step size이다.) 여기서 저자들은 적당한 $\hat{\tau}$값을 제시했고 그게 비록 많은 컴퓨팅 계산시간을 소비할지라도 좋은 퍼포먼스를 보임을 실험적으로 보였다. 저자들이 제안한 값은 다음과 같다. \(\begin{align} \hat{\tau} = \frac{\pi \alpha_{prior}}{2}, \, \text{where } \alpha_{prior}: \text{ standard deviation of prior of parameter} \end{align}\)
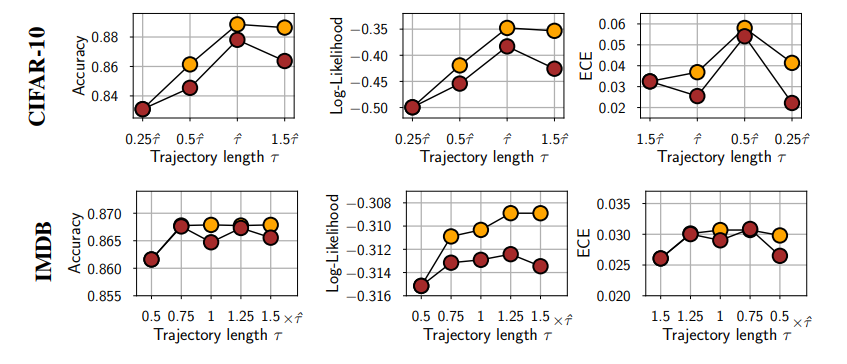
실제 위 실험결과에서 $\hat{\tau}$를 사용했을때 좋은 결과를 얻음을 확인가능했다.
4.2. Step size $\Delta$
이는 각 모수를 업데이트 할때 gradient앞에 곱해지는 학습률로 이해하면 된다. 이는 위에서 설명한것처럼 leap frog 반복횟수와 반비례하는 값이다. 즉 이 값이 작아지면 leap frog 반복회숫는 커지는 관계로 이해할 수 있다. $\Delta$값이 작아지면, 모수의 이동이 더 실제 사후분포에 잘 근사하고 메트로폴리스-헤이스팅스 단계에서 합격확률도 높아지지만, leap frog반복횟수가 커져 계산량이 증가한다는 단점이 있다.
저자들은 총 50번 epochs에 대해 $\Delta = [10^-5, 5 \cdot10^-5, 10^-4, 5 \cdot 10^-4]$으로 해서 실험하였는데 이때 각각의 합격확률이 $[72.2 \%,46.3 \%, 22.2 \%, 12.5 \% ]$로 나옴을 확인하였다. 또한 로그 가능도값 또한 $\Delta = 10^-5$ 이 경우가 가장 크게 나옴을 확인하였다.
Number of HMC chain
이는 독립인 여러 HMC chain을 만든다음, 그것을 하나로 합쳐 사후분포를 근사하는 것을 의미한다. 각각의 chain은 독립이므로 초기값도 각자 다 다를수 있다. 다음 그림을 봤을때 계산 시간이 고정된 경우 하나의 chain만을 사용한것보다 2,3개의 chain을 사용한것의 성능이 더 좋음을 확인가능하다.
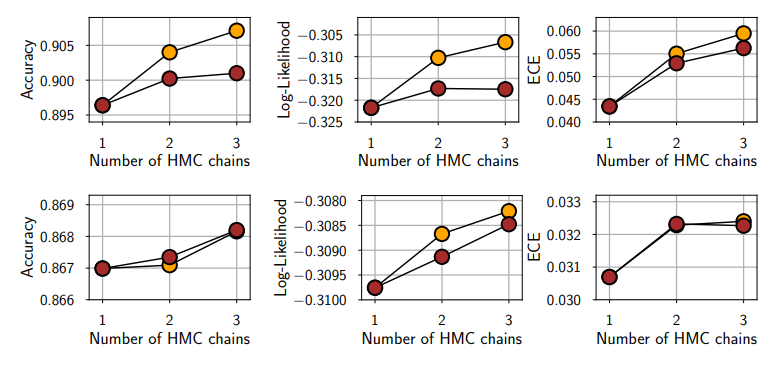
여기서 논문에 쓰인 표현 중 “This result notably shows that HMC is relatively unobstructed by energy barriers in the posterior surface that would otherwise require multiple chains to overcome.” 이란 표현이 있는데 해당 표현에 대해서는 조금 더 생각해봐야 될 것 같다. 아마 이렇게 독립인 chain으로 사후분포를 잘 근사할 수 있는게 사후분포 표면에 있는 에너지 베리어(?)에 의해 HMC가 방해받지 않는다 뭐 이런 말인거 같은데 HMC가 헤밀토니안 역학으로부터 따온 개념임을 고려해봤을 때 그것과 관련된 내용일듯 싶긴한데 구체적으로는 잘 모르겠다.
##
이제 4챕터까지 읽었는데 앞으로 6챕터가 남았고 appendix까지도 있다. Appendix는 아직 읽을까 말까 고민중이긴 한데 아마 본문 내용중에 특히 궁금한 내용이 있지 않는한 이것까지 리뷰할것 같지는 않다. 어째 오늘은 intro에서 결국 저자들이 뭘 하고자 하는지랑 실험셋팅만 주구장창 보다가 끝난거 같은데 다음부터는 본격적으로 어떤 말을 하고자하는지 알아보도록 하자.
11. Reference
1. Izmailov, P., Vikram, S., Hoffman, M. D., & Wilson, A. G. G. (2021, July). What are Bayesian neural network posteriors really like?. In International conference on machine learning (pp. 4629-4640). PMLR.
2. Aitchison, L. (2020). A statistical theory of cold posteriors in deep neural networks. arXiv preprint arXiv:2008.05912.
댓글남기기