논문리뷰: What Are Bayesian Neural Network Posteriors Really Like - 2?

목차

• How well is HMC mixing?
• Evaluating Bayesian neural networks
• Do we need cold posterior?
• Reference

저번 포스팅에 이어서 읽어보도록 하자. 요즘 허리도 안좋고 그 여파로 발 감각도 이상하고 여간 몸상태가 말이 아니다. 운동 다 열심히 하고 좋은 의자 쓰자. 절실히 느끼는 중이다. 또 그와 별개로 최근에 밴처기업과 테스트 프로젝트하는 것이 있는데 그거 때문에 음성 데이터에 적용되는 transformer 중 하나인 wav2vec2.0을 공부하고 있는데 조금 낯선 내용이다 보니까 이해하기가 어렵네. 추후 해당 논문도 정리해서 포스팅해봐야 겠다.

5. How well is HMC mixing?

일단 이 mixing이 뭔지에 대한 문제에 봉착했다. mixture model에서의 혼합을 의미하는 mixing인가? 근데 여기서 그 내용은 크게 상관이 있는것 같지도 않고, 앞부분 내용을 대략 읽어보니 HMC chain의 수렴진단을 어떻게 진행하고 이가 기하적으로 시사하는 바가 뭔지에 대해 알아보는 파트 같은데 해당 용어는 아닌것 같고, 그러면 converging 대신에 mixing을 쓴건가? 이런 생각이 들어 선배한테 여쭤보니, 사후분포가 여러 봉우리(multi modal)인 경우에 각각을 골고루 잘 돌아다닐 수 있는지에 관한 내용이라 한다. 즉, HMC chain이 한곳에서만 계속 왔다갔다 거리는게 아닌 사후분포 전체 영역을 잘 돌아다닐수 있는지에 대한 말로 보면 될 것 같다.

저자들은 weight space와 function space에서의 mixing을 고려하는데, HMC의 경우 function space에서 더 잘 mixing된다는 결론을 내었다.

5.1. $\hat{R}$ diagnostics

겔만-루빈(Gelman-Rubin, 1992) 검정은 동일한 사후분포에서 여러개의 체인을 추출했다고 가정하고 진행한다. 전통적인 ANOVA 검정을 이용하여 체인 내의 분산과 체인 간의 분산을 비교해서 체인 간의 분산이 작다고 판단되면 체인이 수렴했다고 판단한다. 이 때 그 판단 기준으로 검정통계량 $\hat{R}$를 사용하는데 이 값이 1에 가까우면 체인이 잘 mixing되고 수렴했다고 판단한다.

저자들은 이것을 표본추출된 weight의 체인 그 자체와, 그것과 dataset을 사용해 softmax를 먹인 output체인에 대해서 $\hat{R}$값을 구해 히스토그램을 그려봤는데 이는 다음과 같다.

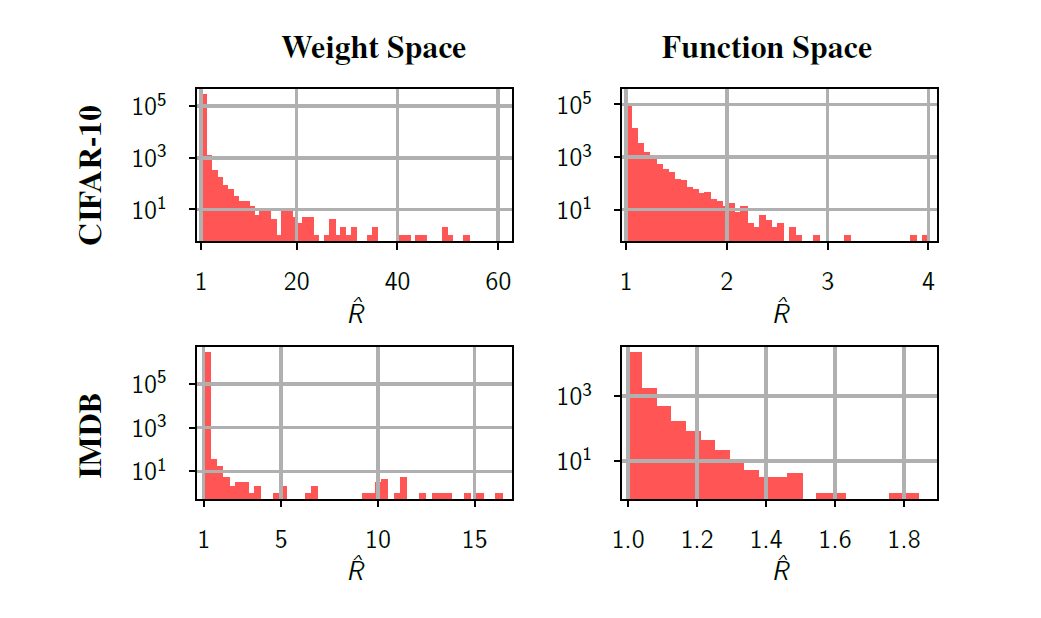
이를 보면 softmax의 결과값으로 나오는 function space에서는 대부분의 chain들에 대해서 $\hat{R}$값이 1.1보다 작음을 확인 가능했다. 이를 통해서 단일 체인이 대부분의 test point의 예측값에 대해서는 다중 체인만큼이나 잘 mixing된다는 걸 확인 가능했다. 이때 weight space에서는 엄청 안좋다라고까진 못해도 몇몇 값들에 대해서는 $\hat{R}$값이 매우 크게 나타나 체인이 mixing에 실패하는 방향이 있음을 알 수 있었다.

5.2. Posterior density visualizations

Weight의 사후분포로부터 추출한 체인중 몇 개의 vector만 골라 이중에서도 2개의 성분에 대해서 시각화한 결과이다.

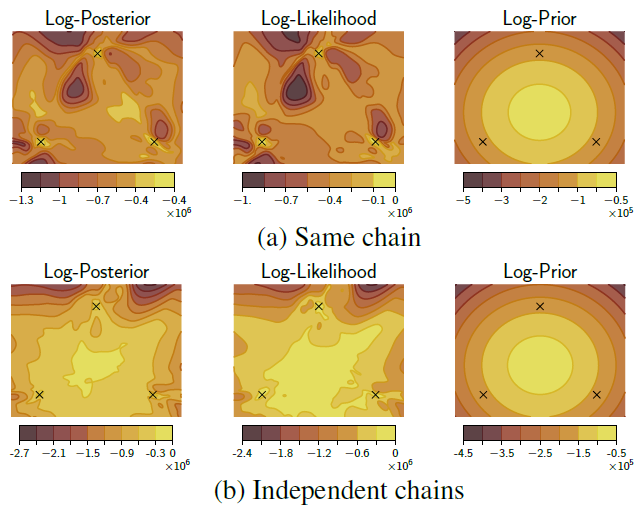
이때 (a)는 한 체인에 대한 시각화이고 세 시점($t=1,51,101$)을 표시하였고 시각화이고 (b)는 세 체인을 통합한 분포에 대한 시각화이고 각 체인에 대해 동일 시점($t=51$)을 표시하였다.

(a)에서 보면 각 샘플들은 각각 다른 mode에 위치해 있음을 확인 가능했다. 즉 한 mode에 간 시점이 있더라도, 그 주변에서만 계속 체인이 생기는게 아닌 다른 mode로 이동할 수 있음을 보여준다. 즉 HMC 표본은 parameter space에서 복잡한 형태의 사후분포를 잘 탐험할 수 있음을 확인가능하다. 이는 unimodal 근사법에 비해 확실한 장점이 될 수 있다.

(b)는 (a)에 비해 보다 정규화되있고 대칭적임을 확인가능한데 이는 위에 5.1.에서 언급한 것 처럼 단일 HMC체인이 weight space에서는 완벽하게 mixing되지 않을수 있음을 시사한다.

5.3. Convegence of the HMC chains

HMC chain에서 burn-in(번인)의 효과를 살펴본 챕터이다. 초기 표본의 경우 사후분포에서 떨어진 영역을 탐색하고 있어 이 값을 추정에 사용하는 것은 오히려 추정값의 정확성에 문제가 될 수 있다. 이런 경우 초기의 적당한 수의 표본을 버리고 나머지를 가지고 추정하는것을 burn-in(번인)이라고 한다. 이를 CIFAR-10과 IMDB data set에 대해 적용시킨 결과는 다음과 같다.

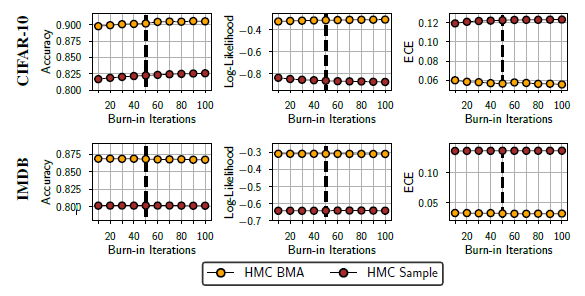
이를 통해 두 경우 모두 burn-in의 효과는 어느정도 시점이후에는 미미하고 그렇기 때문에, 저자들은 실험을 진행하는데 있어 50번째 반복을 기준으로 번인을 적용시켰다고 한다.

6. Evaluating Bayesian neural networks

이번 챕터에서는 이제 본격적으로 BNN의 근본적인 특성에 대해 탐구한다. 이 챕터안에서는 posterior tempering을 시행하지 않았으며, 다시한번 BNN의 성질을 알기 위해 HMC를 사용하는거지 이게 좋다고 주장하는건 아님을 언급한다.

결론부터 요약해서 말하면, BNN은 evaluation과정에서 deep ensemble보다 더 좋은 성능을보이지만, 전통적인 학습 모델에 비해서 도메인 변화에 대해서는 덜 로버스트하다.

6.1. Regression on UCI datasets

Concrete, Yacht, Boston, Energy 그리고 Naval 데이터에 HMC를 적용시키고, 그 결과를 여러 baseline방법들과 비교하였다. 여기서 특징이라한다면 회귀문제에서 fully connected deep neural network 를 적용시켰고, train-test 를 9:1 비율로 나눠 학습과 평가를 진행하였다. 해당결과는 다음과 같다.

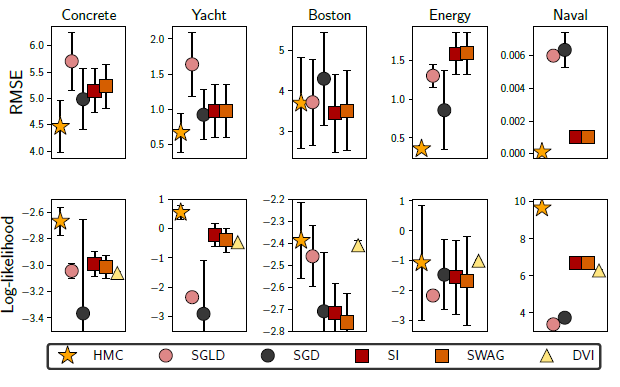
이때 SGLD는 stochastic gradient Langevin dynamics, SGD는 stochastic gradient desent, SI는 subspace inference, DVI는 deterministic variational inference를 의미한다.

대부분의 경우에 RMSE와 log-likelihood 둘의 관점에서 HMC가 다른 방법론보다 더 좋은 성능을 보임을 확인할 수 있었다. 유일하게 Boston 데이터셋에서의 RMSE가 살짝 성능이 비슷하거나 떨어지는 모습을 보이지만 이 경우에도 log-likelihood의 관점에선 다른 방법론들보다 더 성능이 좋았다.

6.2. Image Classification on CIFAR

이미지 분류에서 HMC의 성능을 평가하기 위해 CIFAR-10과 CIFAR-100에 Resnet-20을 적용시켰다. 이와함께 다른 baseline방법들도 같이 적용하였는데 모든 데이터셋 그리고 Accuracy와 log-likelihood 둘다의 측면에서 HMC가 항상 좋은 성능을 보였다.

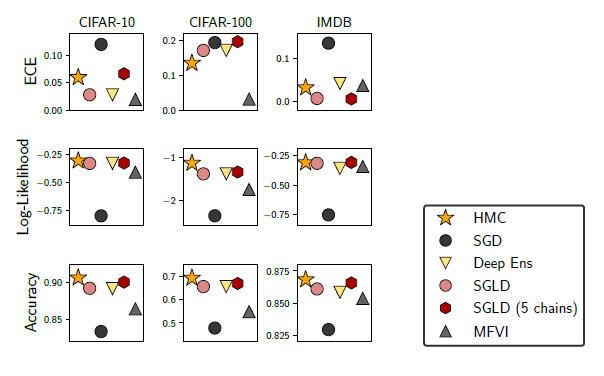
이 경우 저자들은 step size $10^-5$과 prior varinace 1/5를 사용해 한 개의 표본을 만들기 위해서 70,248번의 leapfrog단계를 수행하였다. 또한 각각의 chain에 대해서 번인으로 첫 50개의 표본은 버리고 뒤에 240개의 표본을 사용하였다. 이런 독립인 체인을 3개 만들어 720개의 표본을 사용해 HMC를 진행하였다.

Out-of-distribution dectection

이번 소주제가 꽤나 흥미로웠는데 본래 BNN은 불확실성을 추정해 해당 데이터가 OOD sample인지 아닌지를 확인가능하다. 단, 이번에는 한 데이터를 기준으로 하는게 아닌, 테스트 데이터가 OOD인지를 어떻게 볼 수 있을지와, 그리고 HMC가 얼마나 잘 그것을 식별가능한지를 연구하였다.

이 경우 모델은 CIFAR-10을 통해 학습되었고, 테스트 데이터로는 각각 CIFAR-100과 SVHN을 사용하였다. CIFAR-100은 비교적 CIFAR-10과 비슷하고 SVHN은 더 차이가 남을 상기하자. 이 경우 OOD라고 결정짓는 기준은 predictive confidence(softmax를 통과시킨 값)을 사용하였고 전체적인 성능지표로는 AUC-ROC를 사용하였다. 그 결과는 다음과 같다.

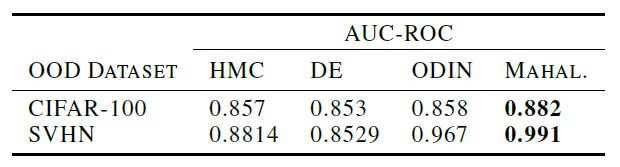
이를 보면 CIFAR-10과 상대적으로 유사한(OOD로 구분하기 어려운) CIFAR-100에 대한 성능은 다른 baseline과 비교해도 떨어지지 않음을 확인가능했지만, SVHN과 같은 더 구분하기 쉬운 OOD인 경우에는 다른 ODIN이나 MAHAL에 비해서 성능이 뒤떨어짐을 확인가능했다.

Robustness to distribution shift

이 경우 BNN이 테스트과정에서 훈련데이터에 노이지가 낀 데이터가 들어왔을때 그 성능이 어떻게됨을 측정한 실험이다. CIFAR-10을 통해 학습을 진행하였고, 이때 CIFAR-10-C를 통해 테스트를 진행하였다. CIFAR-10-C는 CIFAR-10 데이터에 1부터 5까지의 단계로 corruption을 해준걸로 보면된다. 이때 corruption은 총 15개의 종류가 존재한다고 한다. 그 예시로는 아래가 있는데,

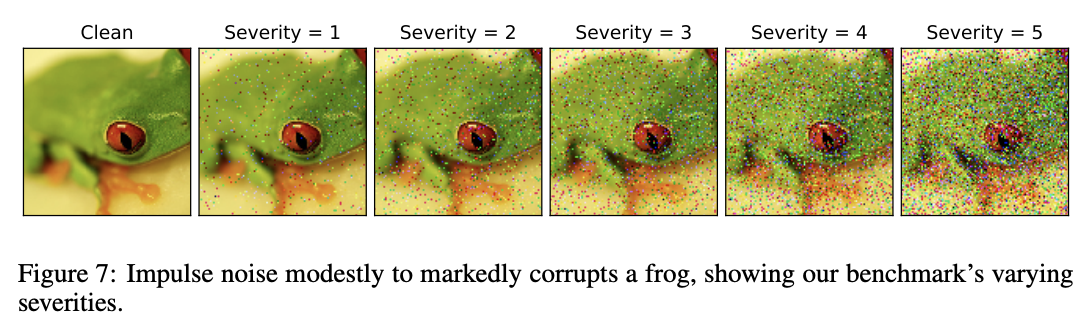
이와 같이 원래의 사진에 여러가지 방법으로 1부터 5까지 단계로 사진을 변형시킨거로 보면 될것 같다. 이런식으로 원본 사진을 이용해 학습을 진행하고, corruption 데이터로 테스트를 한 결과는 다음과 같다.

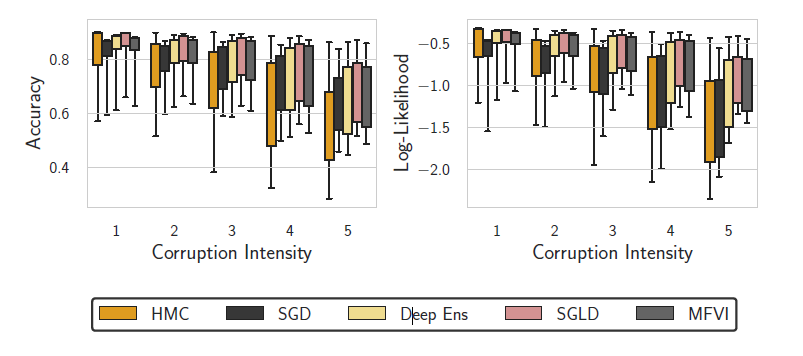
이를 보면 높은 수준의 corruption에서는 HMC는 SGD보다 덜 robust함을 볼 수 있었고, SGLD와 deep ensemble이 HMC보다 더 robust함을 확인가능했다. 다만 흥미로운점은 posterior tempering을 사용하면 corruption robust에서 상당한 성능향상을 보였다.

7. Do we need cold posterior?

다음과 같은 분포를 고려해보자.

\[p_T(w \mid \mathcal{D}) \propto(p(\mathcal{D} \mid w) \cdot p(w))^{1 / T}\]

이런 경우 $T$를 temperature이라 한다. $T=1$인 경우에는 일반적인 BNN의 사후분포 형태가 되고 $T<1$인 경우가 cold posterior, $T>1$인 경우를 warm posterior이라 한다. Cold posterior는 일반적인 사후분포보다 더 sharp해지고 warm posterior는 더 smooth해지는 경향이 있다.

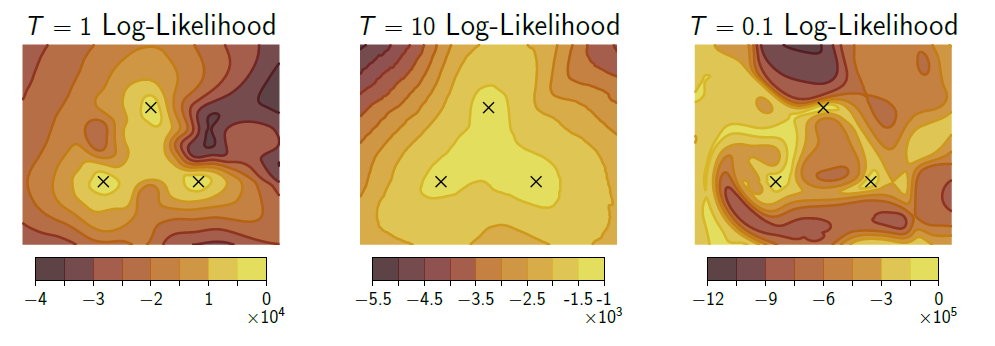
Wenzel(2020)은 BNN이 cold posterior를 필요로하며 $T=1$로 할 시에 일반적인 SGD보다 성능이 더 떨어진다고 주장하지만, 이 논문의 저자들은 이에 대해 의문을 제기한다. 저자들은 cold posterior가 최적의 성능을 달성하는데 거의 필요하지 않으며 오히려 악영향을 줄 수 있다하며, cold posterior의 효과로 보여지는것들은 대부분 data argumentation에 의한것이라 주장한다.

7.1. Testing the cold posterior effect

Wenzel은 cold posterior의 효과를 CIFAR-10에 ResNet-20, IMDB에 LSTM을 적용시켜 실험하였다. 이 실험에서 해당 저자들은 $T=1$에서 성능이 저하됨을 보였는데, 실제 data argumentaion을 진행하지 않고 같은 실험을 진행한다면 $T=1$일 때 거의 최적의 성능을 보인다. 게다가 chapter 6에서 $T=1$일 때 같은 실험상황에서 HMC가 deep ensemble, SGD와 비교했을때 더 성능이 우월함을 보였었다.

또한 $T$의 영향을 조사하기 위해 $T$를 조정해가며 IMDB에 LSTM을 적용시켜 실험하였는데 이때 $T=1$일 때 가장 좋은 성능을 보이고, 이는 심지어 Deep ensemble보다 좋음을 확인하였다.

다만 저자들은 cold posterior가 BNN의 distribution shift에 대한 robustness를 향상시키는데 도움을 준다 말하고, 또한 data argumentation을 통해 data의 개수를 늘렸다면 cold posterior를 사용하는게 더 성능면에서 좋을 수 있다 말한다. Data argumentation를 사용하지 않을때는 cold posterior의 효과를 확인하기 어렵지만 data argumentation를 사용할때는 그대로 사후분포를 사용하는것 보다는 $T<1$로 하는게 합리적이라고 말한다.

##

이번에는 보다 BNN의 성질을 이해하려고하는 실험 위주로 내용이 진행된 것 같다. 이제 거의 끝나가는게 보인다. 이번에는 OOD detection하는거랑 corruption에 관한 내용이 흥미로웠다. 또한 이 논문을 통해서 BNN의 성질을 아는것 자체도 중요하지만 이런 논문을 어떻게 작성하고 실험 셋팅을 어떻게 진행해야하는지 위주로 보는것도 좋은 공부가 될거란 생각이 든다.

11. Reference

1. Izmailov, P., Vikram, S., Hoffman, M. D., & Wilson, A. G. G. (2021, July). What are Bayesian neural network posteriors really like?. In International conference on machine learning (pp. 4629-4640). PMLR.
2. Aitchison, L. (2020). A statistical theory of cold posteriors in deep neural networks. arXiv preprint arXiv:2008.05912.