논문리뷰: What Are Bayesian Neural Network Posteriors Really Like - 3?

목차

• What is the effect of priors in Bayesian neural netrworks?
• Do scalable BDL methods and HMC make similar predictions?
• Discussion
• Reference

드디어 이 논문의 마지막 포스팅이다. 저번에 이어 BNN의 성질을 알아보는데 여기서는 사전분포의 선택이 미치는 영향과 scalable한 BNN 방법들이 실제 HMC와 비슷한 결과를 내는지에 대해 알아본다.

8. What is the effect of priors in Bayesian neural networks?

Bayesian deep learning은 사전분포를 선택하는데 있어 직관적인 설명의 부재로 비난받는다. 보통 그래서 전통적인 베이지안에서는 무정보사전분포(제르피 사전분포 등)을 사용해서 이러한 문제를 해결하려 하지만 BNN에서 그런시도가 있는지는 잘 모르겠다. (대략 찾아보니까 없는거 같기도 한데 이 논문에서는 일단 일반적인 정규분포와, 정규분포와 로지스틱 분포의 혼합분포를 비교하였다.) Wenzel은 많이 사용되는 정규 사전분포 $N(0, \alpha^{2} I)$가 적합하지 않고 성능을 저하시킨다 주정한다. 하지만 이 논문들의 저자는 실제 그렇지 않다고 주장하며 이를 정규분포와 로지스틱 분포의 혼합분포와 비교하며 이와 비교해서도 그렇게 성능이 떨어지지 않는걸 보인다. 이런 과정을 통해 BNN에서 사전분포 선택의 역할에 대해 탐구한다.

8.1. Effect of Gaussian prior scale

일단 사전분포 $N(0, \alpha^{2} I)$에서 $\alpha$의 영향력을 알기위해 이 값을 바꿔가며 실행을 진행하였다. 이때 HMC로부터 40개의 표본만 추출해서 진행하였는데 이는 적은 숫자로 엄청 정확하게 추정을 하기 보단 $\alpha$값들의 영향을 알기 위해 진행한 것임을 명시하고 가자.

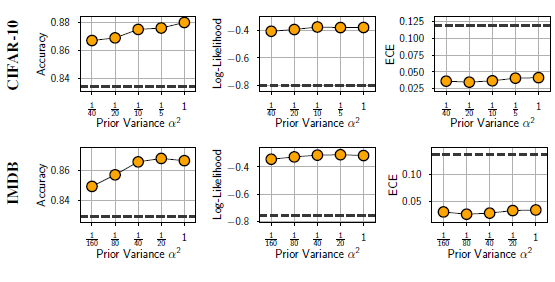
이에서 보면 $\alpha$값이 작을 때 비교적 성능이 잘 나오지 않음을 확인가능하다. 이는 over-regularization의 영향으로 보이며 $\alpha$가 어느정도 커지면 성능차이가 크게 나지 않아 robust함도 확인가능하다. 또한 모든 저 점선은 baseline인 SGD의 성능을 의미하는데 어떤 $\alpha$에 대해서든지간에 일반적인 SGD보단 더 우월함을 볼 수 있다.

8.2. Non-Gaussian priors

이번 소챕터에서는 정규 사전분포와 다른 사전분포를 비교한다. 이때 비교군으로써는 로지스틱 분포와, 정규분포와 로지스틱분포의 혼합분포가 사용되었다. 이때 각 분포는 분산이 1/40이 되도록 스케일된 상황에서 실험을 진행하였다. 그 결과는 다음과 같다.

이를 보면 꼬리부분이 보다 두꺼운 로지스틱분포에서 성능이 제일 좋음을 볼 수는 있으나 그 성능이 정규분포와 비교했을때 큰 차이가 나진 않음을 확인가능 했다.

8.3. Importance of Architecture in Prior Specification

지금껏 우리는 weight에서의 사전분포인 $p(\omega)$에 초점을 맞춰왔지만, 모델 architecture $f(x,\omega)$가 주어졌을때 $p(f(x))$의 사전분포를 고려하는거도 중요하다고 저자들은 말한다. 그래서 오히려 $p(w)$를 정하는건 결과에 큰 차이가 없고 사소한 문제일수 있지만 오히려 architecture가 큰 영향을 미칠 수 있다고 주장한다.

그런데 왜 그런지, 그래서 어떤 가이드라인이 있는지에 대한 설명이 정작 담겨있지 않아서 아쉽다.

9. Do scalable BDL methods and HMC make similar predictions?

앞선 챕터들에서 HMC가 좋은 성능을 보이는걸 보였다. 그런데 실제 문제상황에서는 이러한 HMC를 적용하는게 현실적으로 어려워 다른 Stochastic한 MCMC나 deep ensemble을 많이 사용한다. 이번 장에서는 이러한 방법론들이 실제 HMC와 얼마나 차이가 나는지를 알아보도록 하자.

9.1. Comparing the predictive distribution

이번장에서 HMC로부터 추정한 분포와 다른 방법들로부터 추정한 사후분포를 비교하고, 이들 사이의 거리와 유사도를 구하는데 이때 사용한 유사도로는 argreement그리고 거리로는 total variation을 사용하였다. Agreement는 다음과 같이 정의한다.

\[\frac{1}{n} \sum_{i=1}^n I\left[\arg \max _j p\left(y=j \mid x_i\right)=\arg \max _j q\left(y=j \mid x_i\right)\right]\]

이걸 알기 쉽게 해석해보면, 각 데이터에 대해서 같은 클라스로 구분되는것의 비율로 이해하면 쉬울 것 같다. 분류기 2개가 있다면 그 2개 분류기가 얼마나 비슷하게 분류하는지를 나타내는 측도이다. 그 다음 분포 $p$와 $q$ 사이의 거리를 측정하는 방법 중 하나인 total variation은 다음과 같이 구해진다.

\[\frac{1}{n} \sum_{i=1}^n \frac{1}{2} \sum_j\left|\hat{p}\left(y=j \mid x_i\right)-p\left(y=j \mid x_i\right)\right|\]

이는 원래 두 분포의 total variation이

\(\sup_{A \in \mathcal{A}} | p(A) - q(A) | = \frac{1}{2} \int |p(x) -q(x)| dx\) 로 구해지는 것을 우리에 상황에 맞게 변형하고, 이를 test set에 대해서 추정할 수 있게 만든 형태이다. 각각에 대해서 argreement는 그 값이 커야 두 분포(분류기)가 유사한것이고 total variation은 작아야 유사하다고 판단한다.

이제 이들을 가지고 $p$를 HMC를 사용해 추정한 사후분포 $q$를 비교하고자 하는 방법론에 의해 추정된 사후분포로 설정해 실험을 진행하였다. 이 실험은 학습은 CIFAR-10을 사용해 진행하였고, 테스트는 CIFAR-10-C를 사용하였다.

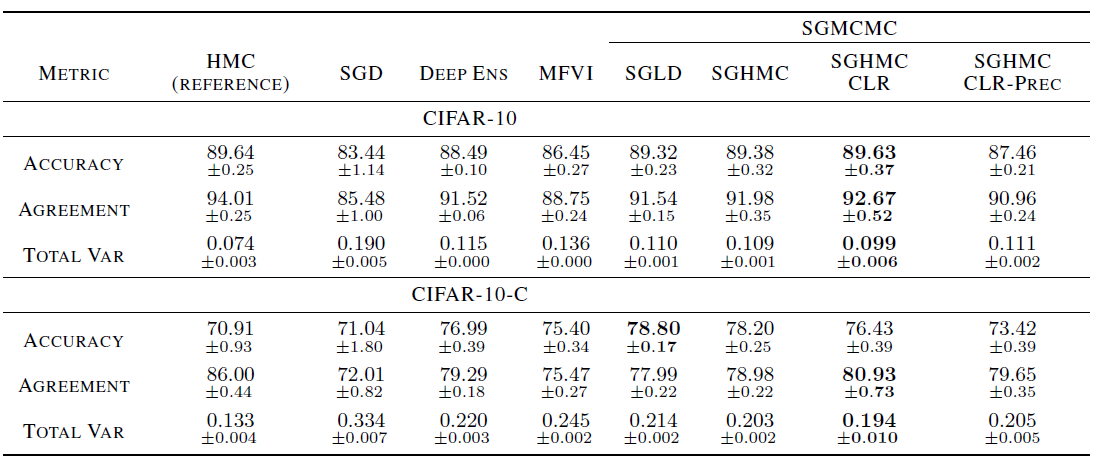
이를 보면 SGLD를 발전시킨 방법인 SGHMC-CLR이 가장 HMC와 유사한것을 볼 수 있었다. 그런데 여기서 눈여겨 볼만한 점은 Deep ensemble은 그 방법자체는 BDL로 구분하진 않지만 이게 Variational inference같은 베이지안 방법보다 HMC에 더 가까운 분포를 만들어냈다는 것이다. 이를 통해 Variational inference를 통해 True 사후분포를 추정하려 할 때는 주의해야 함을 알 수 있다.

또한 CIFAR-10-C에서 보면 SGHMC-CLR의 성능이 비교적 떨어지는데 이는 이게 HMC와 유사한 사후분포를 추정하다보니 이전 챕터에서 HMC의 단점중 한개인 covairate-shift에 대해 robust하지 않은 성질을 가지고 있어서 그런거로 추측된다.

9.2. Predictive entropy and calibration curves

이번에는 위에 나온 방법론들이 over-confident에 대해 얼마나 내성이 있는지 알아보기 위한 실험을 진행하였다. 각 추정된 사후분포에 대해 Predictive entropy and calibration curves을 구하였다. 이때 Predictive entropy는 0에 가까운 수치가 많으면 보다 over-confident하고 calibration curves에서는 0보다 작으면 over-confiden하고 0보다 크면 under-confidnet하다고 보면 된다.

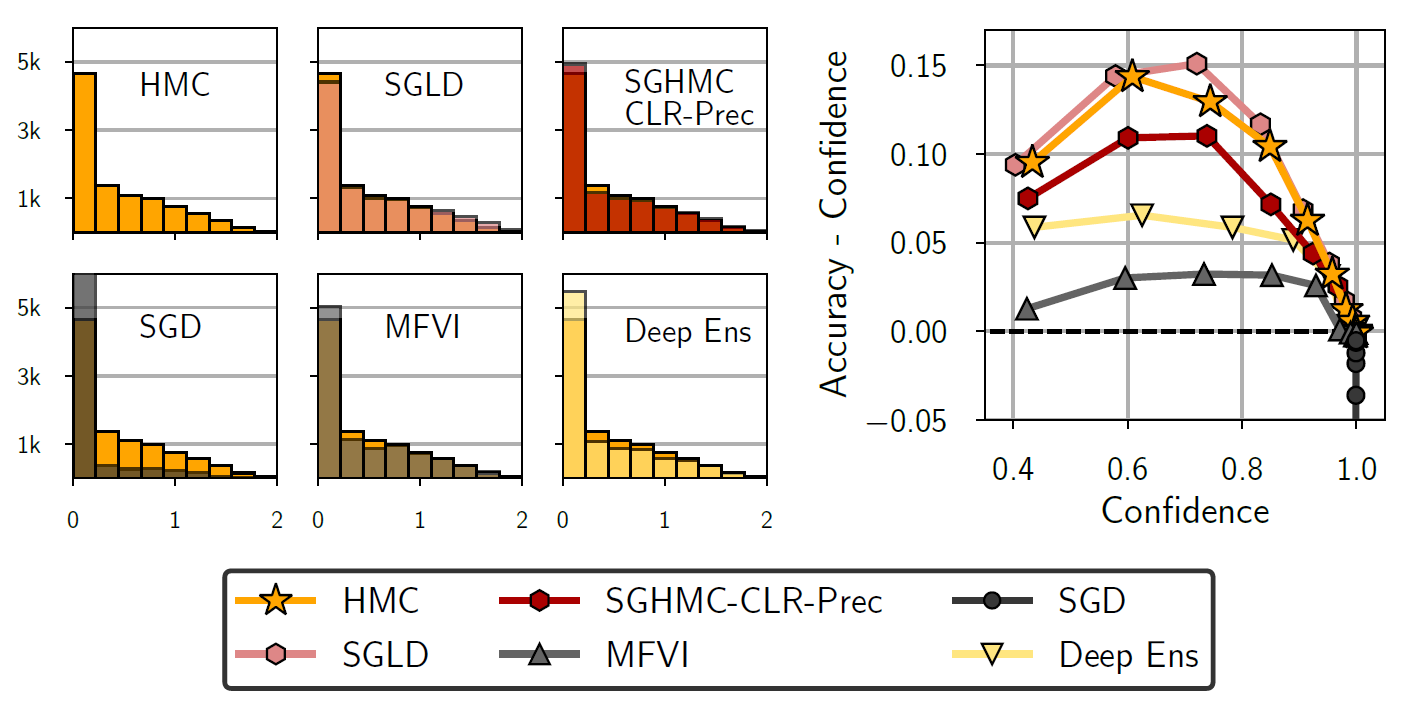
이 결과를 보면 SGD를 제외하면 나머지 방법들은 꽤나 보수적임을 확인가능했다. SGD는 널리 알려진것 처럼 over-confident함을 보였다. SGLD는 HMC보다 살짝 under-confident하며 SGHMC-CLR-Prec는 상대적으로 over-confident했다. 그리고 오른쪽의 calibration curves를 보면 SGLD와 SGHMC-CLR-Prec는 HMC와 비슷하게 나오는 반면 MFVI와 Deep ensemble이 가장 calibrate함을 확인가능했다.

10. Discussion

이 논문에서는 full batch HMC를 사용해 BNN의 사후분포를 최대한 정확하게 추정해 그에 대한 성질을 밝히고자 하였다. 이게 실제 상황에서 적용되긴 어려울지라도 이를 통해 BNN의 성질을 탐험하는 것 자체가 큰 의미를 가진다고 생각한다. 또한 저자들은 기존 통설을 그대로 받아들이면 안된다고 주정하는데, 이 논문에서도 기존의 cold-posterior를 사용해야하고 와 정규 사전분포가 좋지 않다는 것에 의의를 제기하였다.

내 생각에는 이 논문에서 특별한 방법론을 제시하진 않았고, 사용한 방법 또한 실제 상황에 적합하진 않지만 앞으로 논문을 작성하는데 있어서, 어떻게 작성해야하는지 공부할 수 있던 기회가 된것 같다. 단순히 BNN의 성질이 이런게 있구나 에서 멈추지 않고 어떤식으로 실험을 설계해서 이를 주장하였는지를 공부하면 좋을 것 같다.

11. Reference

1. Izmailov, P., Vikram, S., Hoffman, M. D., & Wilson, A. G. G. (2021, July). What are Bayesian neural network posteriors really like?. In International conference on machine learning (pp. 4629-4640). PMLR.