목차

  • Introduction
  • Basic Idea
  • pSGLD
  • Summary

이 블로그에는 포스팅하지 않았지만 이전에 Dropout을 사용해 Bayesian nueral network를 학습시키는 MC-dropout(Gal, 2016)에 대해서 공부한적있었다. 기본적으로 BNN에서 weight $\omega$에 대한 사후분포를 학습하려는게 목적인데 이것이 closed form으로 존재하지 않아 크게는 두가지 방법

  • MCMC
  • Variational inference

를 사용하는데 이때 MCMC를 사용하는것이 이전에 포스팅했던 SGLD나 SG-HMC같은 방법들이고, MC-dropout은 Variational inference를 사용한다. 이때 주 목적은 사후분포 $p(\omega \mid \mathcal{D})$를 근사하는 변분분포 $q(\omega \mid \theta)$를 추정하는 것이다. 이때 MC-dropout은 일반적인 DNN에 Dropout regularization을 적용한 것이 변분분포로 근사될 수 있음을 보여 BNN을 적합하였다. 오늘 공부할 Bayes by backprop는 이와 달리 보다 직접적으로 KL divergence에 역전파를 사용해 변분분포를 적합하는것으로 이해하면 될 것이다.

1. Introduction

기존에 많이 사용하는 DNN의 경우 많은 parameter를 사용하고 모델이 복잡해짐에 따라 training data를 그대로 기억함으로써 overfitting되서 일반화능력이 떨어지는 경향이 있다. 또한 이 경우 overconfident하는 경향이 있다. 이런 문제를 해결 하기 위해 regularization 기법을 사용하는데 그 중 한 개가 weight의 사전분포를 고려하는 것이다. 이 논문의 경우 단순히 사전분포를 regulization term으로 주는것에서 끝나지 않고 이를 사용해 weight의 사후분포를 구하는게 목적이다. 이렇게 하면 각 추론의 uncertainty 까지 고려가능해 보다 regularization 효과를 높일 수 있다.

그러기 위한 방법으로 Bayesian 방법론중 하나인 variational inference를 사용해 사후분포를 근사하는 $\theta$로 parameterized 된 변분분포 $q(\omega \mid \theta)$ 고려한다. 이후 이와 사후분포 사이의 거리를 최소로하는 $\theta$ 를 최적화 한다. 저자들은 이 방법을 “Bayes by Backprop”라고 명칭한다.

기존에 Uncertainty를 고려하기 위한 방법으로 model ensemble이 많이 사용됐는데 이 경우 한 모델에 사용되는 parameter의 수가 $p$ 개라 한다면 ensemble 모델을 $m$개 적합한다 하면 $p \cdot m$ 개의 parameter을 학습해야하는 반면, BBP는 $2 \cdot p$ 개의 parameter만 학습하고 이후 변분분포부터 weight를 추출하기만 하면되서 보다 효율적이다.

저자들은 BBP가 강화학습에도 도움이 된다고 주장하지만 해당부분에 대해서는 내 관심사가 아니므로 이번 포스팅에서는 다루지 않을 것이다.

2. Basic Idea

원래 기존 논문에서는 2절에서 짧게 기존의 point estimate를 하는 DNN에 대해서 다루지만 이건 너무 많이 알려진 내용이고 굳이 할애를 할 필요가 없다 생각하고 이보단 BNN의 기본 Idea를 설명하는게 더 유의미하다 생각한다.

png

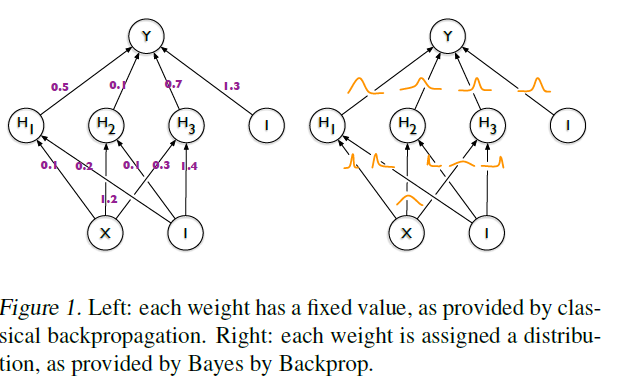
기본적으로 DNN에서 weight는 고정된 값으로 간주된다. 다만 이럴 경우 점추정밖에 불가능하고 추정량의 변동성 즉 불확실성(uncertainty)를 추정하는게 불가능해진다. 특히 이게 직관적으로 문제가 되는 부분은 train data가 있지 않은 부분에서 overconfident한 예측을 해 잘못된 의사 결정으로 이끌 가능성이 있다. BNN은 이런 문제를 해결 하기 위해서 각 weight에 분포를 줘 weight를 한 값으로 예측하는 것이 아닌 해당 분포 자체 추정한다(Figure1).

이럼으로써 다음 그림(Figure5)와 같이 점추정뿐 아니라 불확실성을 추정해 의사결정에 보다 도움을 줄 수 있다.

png

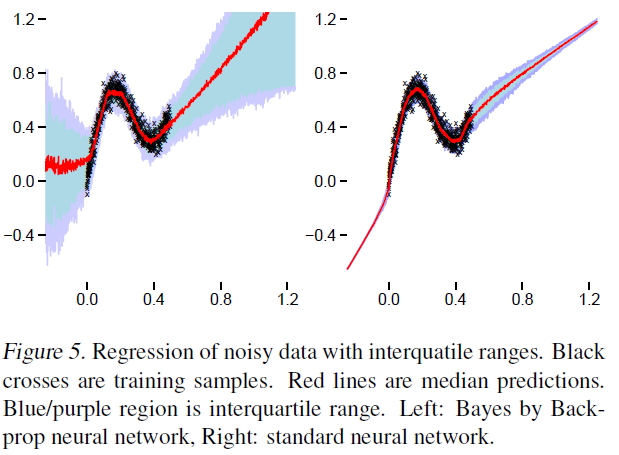
위 그림에서 좌측이 BNN, 우측은 일반적인 DNN을 적합한 것이다. 보면 데이터가 없는 부분, 예컨데 $x<0$ 혹은 $x>0.8$ 인 경우 training data가 거의 없어 해당 부분에서는 불확실성이 커야하는데 DNN의 경우 그걸 모르고 confident하게 해당 빨간값으로 답을 도출해버리는 단점이 있다. 반면 우측에서 보면 BNN은 해당부분에서 uncertainty가 크게 나타남으로써 단순히 한 점으로 추정하면 안된다는 것을 알 수 있다. 이러한 장점들이 있기 때문에 여러 계산상의 이슈에도 불구하고 BNN을 적합하려는 시도들이 꾸준히 이뤄지고 있다.

3. Being Bayesian by Backpropagation

위에서도 간략하게 언급한것처럼 weight의 사후분포 $P(\omega \mid \mathcal{D})$와 이를 근사하는 변분분포 $q(\omega \mid \theta)$의 거리를 최소로 하는 $\theta$를 최적화한다. 이때 거리는 KL divergece로 사용해 다음과 같은 식을 얻을 수 있다.

\[\begin{aligned} \theta^{\star} & =\arg \min _\theta \operatorname{KL}[q(\omega \mid \theta) \| P(\omega \mid \mathcal{D})] \\ & =\arg \min _\theta \int q(\omega \mid \theta) \log \frac{q(\omega \mid \theta)}{P(\omega) P(\mathcal{D} \mid \omega)} \mathrm{d} \omega \\ & =\arg \min _\theta \operatorname{KL}[q(\omega \mid \theta) \| P(\omega)]-\mathbb{E}_{q(\omega \mid \theta)}[\log P(\mathcal{D} \mid \omega)] \end{aligned}\]

여기서 마지막 비용함수는 “Expected lower bound” 다른 말로 “ELBO”라는 용어로 많이 알려져 있다. 간략하게 쓰면 다음과 같다.

\[\begin{align} \mathcal{F}(\mathcal{D}, \theta)=\mathrm{KL}[q(\omega \mid \theta) \| & P(\omega)] \nonumber \\ & -\mathbb{E}_{q(\omega \mid \theta)}[\log P(\mathcal{D} \mid \omega)] \end{align}\]

$\mathcal{F}(\mathcal{D}, \theta)$를 최소로 한다는 것의 의미를 생각해보자. 일단 $\mathbb{E}_{q(\omega \mid \theta)}[\log P(\mathcal{D} \mid \omega)]$ 값을 크게 한단 것인데 이는 data에 대한 가능도를 높이는것이니 주어진 training data에 맞게 복잡한 모델을 적합시킨단 것이다. 반면 그러면서 $\mathrm{KL}[q(\omega \mid \theta) | P(\omega)]$를 작게 만드는데 이는 변분분포를 주어진 간단한 사전분포와 비슷하게 만든단 것이므로 규제효과를 준다고 이해할 수 있다.

실제 $\mathcal{F}(\mathcal{D}, \theta)$를 계산하는것은 불가능하기 때문에 경사하강법과 Monte Calro sampling을 통해 이를 근사해서 최적화를 진행하다.

3.1. Unbiased Monte Carlo gradients

해당절에서는 경사하강법에서 gradient를 계산할 때 이를 Monte Calro sampling을 사용해 계산해도 되는 이론적 근거와 이를 보다 계산하기 쉽게 하기 위한 reparameterized trick을 소개한다.

Reparameterized trick은 진짜 말그대로 trick 눈속임이고 이름이 붙은거에 비해서 진짜 거창한게 없으니 겁먹지 말자. 쉽게 설명하면 $\omega \sim N(\mu, \sigma^{2})$으로부터 표본추출할 때 이로부터 추출하는게 아니라 $\epsilon \sim N(0, 1)$로부터 $\epsilon$을 추출하고 $\omega = \sigma \epsilon + \mu$ 이렇게 $\omega$를 표본추출하는 것을 의미한다. 어떻게 보면 조삼모사처럼 생각될 수 있지만 이렇게 할 시에 분포자체를 최적화시킨다는 생각으로부터 단순히 paramerter들만 최적화시키면 된다는 스탠스로 바뀌는데 이점이 있다. 이 예시에는 $\epsilon$이 따르는 분포인 $N(0,1)$을 $q(\epsilon)$ 그리고 $\theta = (\mu, \sigma)$, $t(\theta, \epsilon) = \sigma \epsilon + \mu$ 로 일반화시켜 생각할 때 다음이 성립한다.

Proposition 1. 확률 밀도 함수가 $q(\epsilon)$로 주어지는 확률 변수 $\epsilon$을 고려하고, $\omega=t(\theta, \epsilon)$이며 $t(\theta, \epsilon)$가 결정론적 함수인 경우를 가정하자. 더 나아가, 주변 확률 밀도 $q(\omega \mid \theta)$가 $q(\epsilon) d \epsilon=q(\omega \mid \theta) d \omega$인 경우를 가정하자. 그런 다음 $\mathrm{w}$에서 미분 가능한 함수 $f$에 대해 다음이 성립한다:

\[\frac{\partial}{\partial \theta} \mathbb{E}_{q(\omega \mid \theta)}[f(\omega, \theta)]=\mathbb{E}_{q(\epsilon)}\left[\frac{\partial f(\omega, \theta)}{\partial \omega} \frac{\partial \omega}{\partial \theta}+\frac{\partial f(\omega, \theta)}{\partial \theta}\right]\]

이는 특정 조건에서 미분과 적분이 순서교환 가능한것을 사용하면 쉽게 증명할 수 있다. 관심있는 사람은(Blundell, 2015)를 참고하도록 하자.

이를 직관적으로 설명하면 평균의 gradient를 구한것과 평균을 하기전 gradient를 구하고 평균을 한것이 동일하단 의미로 다시 말해서 loss function의 gradient가 cost function의 gradient의 불편추정량이 된다는것을 의미한다. 즉 이는 경사하강법에서 Monte Calro sampling을 사용하는 이론적인 근거가 된다.

Proposition 1을 (1)에 적용시키기 위해서는 단순히 $f(\omega, \theta) = \log q(\omega \mid \theta) - \log P(\omega)P(\mathcal{D} \mid \omega)$로 하면 된다.

3.2. Algorithm of BBP when using gaussian variational posterior.

이제 변분분포를 각 weight가 독립이고 동일한 평균과 분산을 가지는 정규분포로 가정하자. 이 경우 분산 $\sigma$는 항상 양수이므로 $\sigma = \log (1 + \exp(\rho))$의 형태로 계산하도록 하자. 그러면 이때 최적화되는 parameter은 $\theta = (\mu , \rho)$ 이다. Reparameterization을 사용해 이를 표현하면 다음과 같다.

\[\omega = t(\theta, \epsilon) = \mu + \log(1 + \exp(\rho)) \circ \epsilon \quad \text{when } \epsilon \sim N(0,I)\]

이를 사용한 최적화 알고리즘은 다음과 같다.

  1. Sample $\epsilon \sim \mathcal{N}(0, I)$.
  2. Let $\omega=\mu+\log (1+\exp (\rho)) \circ \epsilon$.
  3. Let $\theta=(\mu, \rho)$.
  4. Let $f(\omega, \theta)=\log q(\omega \mid \theta)-\log P(\omega) P(\mathcal{D} \mid \omega)$.
  5. Calculate the gradient with respect to the mean
\[\Delta_\mu=\frac{\partial f(\omega, \theta)}{\partial \omega}+\frac{\partial f(\omega, \theta)}{\partial \mu} .\]
  1. Calculate the gradient with respect to the standard deviation parameter $\rho$
\[\Delta_\rho=\frac{\partial f(\omega, \theta)}{\partial \omega} \frac{\epsilon}{1+\exp (-\rho)}+\frac{\partial f(\omega, \theta)}{\partial \rho} .\]
  1. Update the variational parameters:
\[\begin{aligned} & \mu \leftarrow \mu-\alpha \Delta_\mu \\ & \rho \leftarrow \rho-\alpha \Delta_\rho . \end{aligned}\]

이 때 $\frac{\partial f(\omega, \theta)}{\partial \omega}$은 평균과 분산의 gradient에 공유되어 있고 일반적인 DNN에서 gradient를 구한것과 동일함에 주목하자. 결국 평균과 분산의 gradient를 구한다는건 DNN에서 gradient를 계산하고 이를 scale하고 shift한것과 동일함에 주목하자.

여기서 한가지 내가 개인적으로 드는 의문점은 이건 결국 cost function의 gradient를 Monte Calro를 사용해서 추정한것인데 보면 한번의 반복시에 $\epsilon$을 한번만 표본추출함을 확인가능하다. 보통의 Monte Calro라 하면 여러번 표본추출해서 이에대한 평균으로 추정하는데 여기선 그러지 않고 단 하나의 표본만 사용했다는 점에서 의문이 남는다.

3.3. Scale mixture prior

이제 사전분포를 어떻게 설정할것인지에 대해서 짧게만 언급하고 넘어가자. 사전분포 $p(\omega) \sim N(0, \sigma_{1}^{2})$ 이라 한다면 여기서도 모르는 모수 $\sigma_{1}$을 대체 어떻게 처리하면 좋을까. 일단 처음 드는 생각은 변분분포의 paraemter 처럼 최적화시키는걸 생각할 수 있다. 그런데 이 방법은 그닥 효율이 좋지 않음이 알려져 있다. CROSS-validation이나 아니면 Epirical bayes를 적용시켜서 추정할 수도 있을 것이다. 다만 이 경우 굳이 그렇게 하기 보단 $\sigma_{1}$을 hyperparameter로 설정하고 적당한 값을 잡아서 초기에 학습이 잘 진행되면 그 값을 사용하고 그렇지 않다면 다른 값을 넣어보고 이런식으로 하는걸 저자들은 권장한다.

또한 단순히 가우시안 사전분포를 사용하는것으로부터 벗어나기 위하여 혼합 가우시안 분포를 사용하는것을 제안한다.

3.4. Minibatches and KL re-weight

Scalable한 model을 만들기 위해 통상적인 DNN에서 SGD를 사용하듯 BBP역시 minibatch 최적화가 가능하다.

(1)의 식에서보면 가능도항에 데이터셋 $\mathcal{D}$가 포함되늰데 이를 각 batch를 무작위로 나눠 계산가능하다.

이 경우 각 batch에 대한 cost function은 다음과 같다.

\[\begin{align} \mathcal{F}_i^\pi\left(\mathcal{D}_i, \theta\right)=\pi_i \mathrm{KL}[q(\mathbf{w} \mid \theta) & \| P(\mathbf{w})] \nonumber \\ - & \mathbb{E}_{q(\mathbf{w} \mid \theta)}\left[\log P\left(\mathcal{D}_i \mid \mathbf{w}\right)\right] \end{align}\]

이 때 $\sum_{i=1}^{M} \pi_{i} =1$을 만족해야 하며 저자들은 $\pi_i=\frac{2^{M-i}}{2^M-1}$를 사용할 것을 추천한다. 이는 i가 커짐에 따라 $\pi_{i}$는 감소하는데, 데이터를 많이 접하지 않은 초반에는 사전지식(사전분포)의 영향을 크게 받다가, 데이터를 많이 본 후에는 데이터셋의 영향을 더 많이받는다는 것으로 이해하면 좋을 것 같다.

4. Summary

BBP는 variational inference와 경사하강법을 사용해 사후분포를 근사하는 방법론이다. $\hat{\theta}$를 학습하는데 성공하였다면 그 후 $q(\omega \mid \hat{\theta})$를 통해 $\omega$ 를 표본추출하여 prediction에 대한 예측은 표본평균으로 불확실성은 표본분산(혹은 표본표준편차)로 계산가능하다. 이런 방법으로 예측에 대한 불확실성을 추정가능하고, 기존 DNN에 regularization을 준거로 해석하여 보다 성능을 개선시킬 수 있다.

5. Reference

1. Blundell, Charles, et al. "Weight uncertainty in neural network." International conference on machine learning. PMLR, 2015.
2. Gal, Yarin, and Zoubin Ghahramani. "Dropout as a bayesian approximation: Representing model uncertainty in deep learning." international conference on machine learning. PMLR, 2016.

댓글남기기

참고