CYCLICAL STOCHASTIC GRADIENT MCMC FOR BAYESIAN DEEP LEARNING
목차
- Introduction
- Preliminaries:SG-MCMC
- Cyclical SG-MCMC
- Theoretical Analysis
- Experiment
- Summary
석사 졸업 논문 초고 작성하다 흥미로운 내용이 있어 해당 논문을 공부해보려 한다.
1. Introduction
심층신경망의 가중치의 사후분포는 대부분의 경우 고차원이며 multi-modal(convex하지 않고 여러개의 봉우리가 존재)인 경우가 많다. 그래서 이 사후분포로부터 가중치를 추출하려 하면 국소적인 최대 혹은 최소지점에 갇혀 다른 부분을 표본추출 하지 못하는 경우가 생긴다. 이를 해결하기 위해선 학습률을 크게 잡아야하지만, SGLD를 포함한 확률적 몬테카를로 방법에서는 반복을 진행할 때마다 학습률을 작게해야 수렴성이 보장되기 때문에 지속적으로 학습률을 크게 하기 어렵다는 문제점이 있다.
해당 논문은 이를 해결하기 위해 Cyclical learning rate scheduler를 사용하는 방법을 제안한다.
2. Preliminaries:SG-MCMC
SG-MCMC에는 크게 두가지 방법이 있는데 하나는 해밀토니안 몬테카를로를 바탕으로한 SG-HMC와 다른 하나는 랑쥬빈 몬테카를로를 바탕으로한 SG-SGLD가 있다. SG-SGLD에 대해서는 이전에 다룬 포스팅이 있으니 해당 내용 참고해주면 될 것 같다. 핵심만 요약해서 말하면 사후분포로터 표본을 추출하는데 이 경우 전체 데이터에 대한 가능도를 사용하면 너무 계산량이 많아지므로 sgd의 방법론을 받아드려, mini-batch로 데이터를 나눠 이로부터 표본을 추출하는 방법론을 칭한다.
이 때 추출된 표본이 사후분포로 수렴하기 위해서는 다음 가정을 만족해야 한다.
Assumption 1. The step size ${\alpha_{k} }$ are decreasing, i.e., $0<\alpha_{k+1}< \alpha_{k}$, with $1) \sum_{k=1}^{\infty} \alpha_{k} = \infty ; \text{and} 2) \sum_{k=1}^{\infty} \alpha_{k}^{2} < \infty$.
3. Cyclical SG-MCMC
위 처럼 학습률이 작아지는데 local mode에 갇힌 경우 여기서 벗어나기 위해서는 많은 수의 반복이 필요하다. 즉 다시말해 계산량이 많아지는 문제가 생긴다. 이를 해결하기 위해 해당 논문의 저자는 Cyclical learning rate scheduler를 다음과 같이 코사인 함수를 이용해 제시한다.
$k$번째 반복의 학습률을 다음과 같이 정의한다.
\[\begin{align} \alpha_{k} = \frac{\alpha_{0}}{2} \left[ \cos \left( \frac{\pi \text{ mod}(k-1, K/M)}{K/M} \right) + 1\right], \end{align}\]여기서 $M$ 은 한 주기안에 속하는 반복의 횟수이고, $K$는 전체 반복 횟수를 의미한다.
흥미로웠던점은 여기서 각 주기마다 burn-in을 적용한다는 점이었다. 각 주기안에서 학습률이 큰 초기에는 사후분포에서 확률밀도가 높은 곳을 찾아가는 단계(Exploration Stage), 그리고 어느정도 반복이 진행되 새로운 local mode를 찾아내고 학습률이 충분히 작아진 다음에는 그 mode를 구체화해 표본을 추출하는 단계(Sampling Stage) 이 두 단계로 나눠서 반복해 표본추출을 진행하는게 가장 흥미로웠다.
이를 Epoch($k$)에 대한 그래프로 나타내면 다음과 같다.
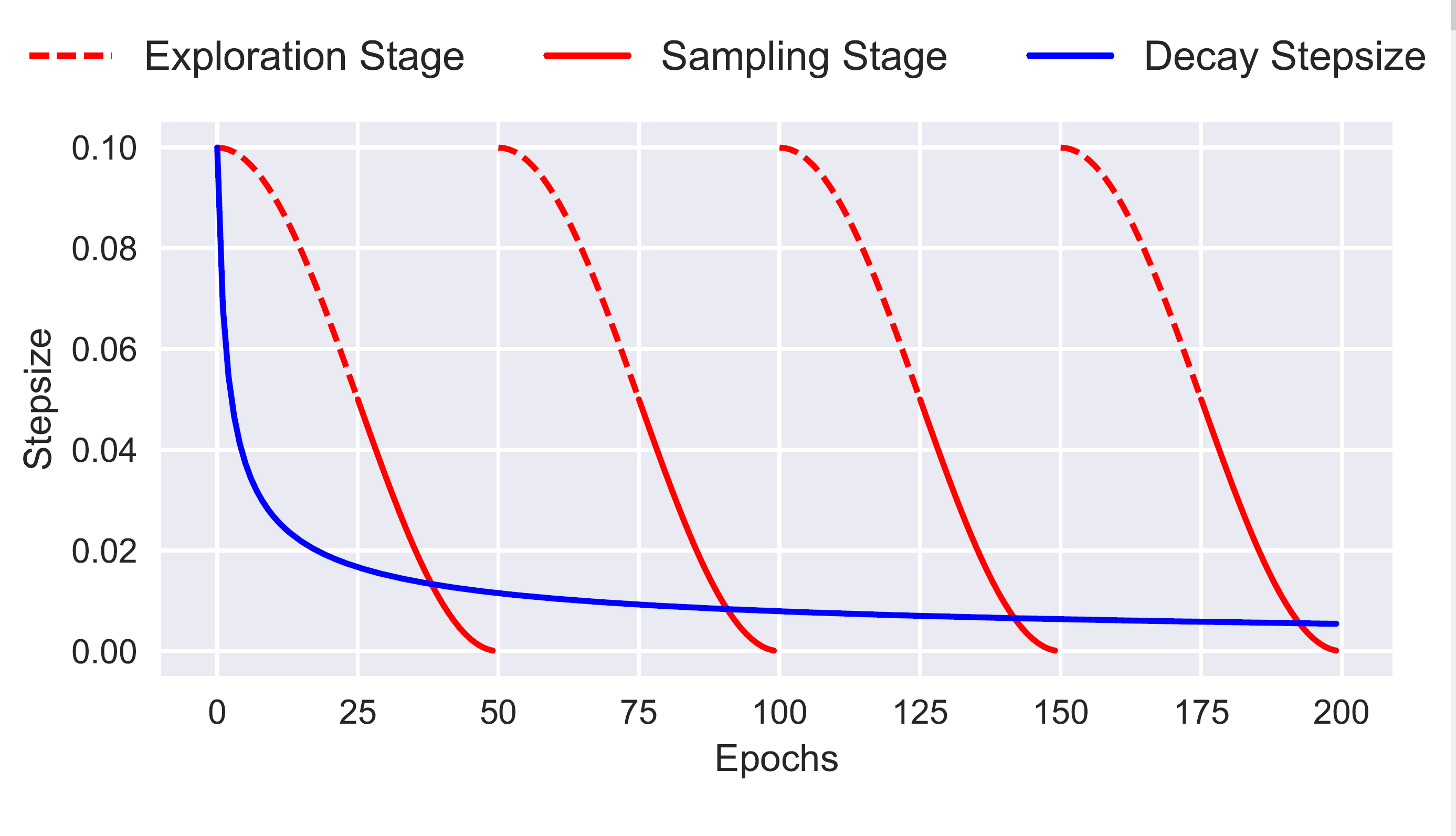
전체 과정을 알고리즘으로 쓰면 다음과 같다.
Alogorithm 1. Cyclical SG-MCMC
Input: The initial stepsize $\alpha_{0}$, number of cycles $M$, number of training iterations $K$ and proportion of exploration stage $\beta$.
$\quad$ for k=1:K do
$\qquad \alpha \leftarrow \alpha_{k}$ according to Eq (1).
$\qquad \mathbf{if} \, \, \frac{ \text{ mod}(k-1, K/M)}{K/M} < \beta \text{ }\mathbf{then}$
$\qquad \quad \% \text{ Exlploration stage}$
$\qquad \quad \theta \leftarrow \theta -\alpha \nabla \tilde{U}_{k} (\theta)$
$\qquad \mathbf{else}$
$\qquad \quad \% \text{ Sampling stage}$
$\qquad \quad \text{ Collect samples using SG-MCMC methods}$
Output: Samples ${\theta_{k} }$
이전에는 multi-modal분포로 부터 표본추출을 하기 위해서는 초기값을 여러개로 설정해서 여러개의 마코프체인을 추출하는 방법을 사용했었다. 이런 경우 마코프 체인을 $m$개를 추출한다고 하면 체인의 개수 * 체인의 길이 만큼의 계산량이 필요했지만, 위 방법을 사용하면 하나의 체인만으로 multi-modal분포로 부터 표본추출이 가능하기 때문에 계산상에서 이점이 있다.
4. Theoretical Analysis
Cyclical learning rate scheduler를 사용한 SG-MCMC로부터 추출한 표본이 사후분포로 수렴하는것을 두가지 측면에서 보였다. 한 가지는 추출한 표본으로부터의 경험적 분포가 사후분포로 weak convergence 하는 것이고 다른것은 경험적 분포와 사후분포 사이의 거리가 유계가 되는것을 보였다. 여기서 분포사이의 거리는 Wasserstein distance를 사용하였다.
해당 파트는 내가 아직 잘 공부하지 못한 측면도 있고 생각을 해봤을때 개인적으로는 납득되지 않는 부분이 있어 해당부분에 대해서 설명해보려고 한다.
4.1. Weak Convergence
여기서 저자들이 보인것과 내가 알고있는것과의 괴리감이 있어서 지금 당장은 납득이 잘 가지 않는 상황이다. 유계이고 연속인 함수 $\phi$에 대해서
\[\bar{\phi} \triangleq \int_{\mathcal{X}} \phi(\theta) \rho(\theta) \mathrm{d} \theta , \quad \hat{\phi}=\frac{1}{K} \sum_{k=1}^K \phi\left(\theta_k\right)\]이렇게 정의할 때 다음 정리가 성립한다는걸 저자들이 증명하였다.
Theorem 1. Under Assumptions 2 in the appendix, for a smooth test function $\phi$, the bias and MSE of cSGLD are bounded as: \(\begin{align} \text { BIAS: }|\mathbb{E} \tilde{\phi}-\bar{\phi}|=O\left(\frac{1}{\alpha_0 K}+\alpha_0\right), \quad M S E: \mathbb{E}(\tilde{\phi}-\bar{\phi})^2=O\left(\frac{1}{\alpha_0 K}+\alpha_0^2\right) \end{align}\)
여기서 $K \rightarrow \infty, \alpha_{0} \rightarrow 0$ 를 해주면 각각이 0으로 수렴하고 이로부터 $\tilde{\phi} \overset{p}{\rightarrow} \bar{\phi}$ 임은 성립하지만 이게 $\tilde{\phi} \rightarrow \bar{\phi} \,\, a.s.$ 임을 의미하지는 않는다. 여기서 weak convergence를 보이기 위해선 저게 확률수렴하는 것이 아닌 그보다 강한 almost surely 수렴해야하는데 여기서 내가 알고있는 것과는 달라 이해가 어렵다. 이는 추후 Appendix를 공부해야 더 잘 이해할 수 있을 것 같다.
4.2. Convergence under the Wasserstein distance
두 분포사이의 거리를 Wasserstein distance로 다음과 같이 정의하자.
\[W_2^2(\mu, \nu):=\inf _\gamma\left\{\int_{\Omega \times \Omega}\left\|\theta-\theta^{\prime}\right\|_2^2 \mathrm{~d} \gamma\left(\theta, \theta^{\prime}\right): \gamma \in \Gamma(\mu, \nu)\right\}\]이 때 $\mu_{K}$를 추출된 표본으로부터 만든 경험적 분포의 확률측도로 정의하고, $\nu_{\infty}$를 타겟 사후분포의 확률측도로 정의하면 다음이 성립하는 것을 증명했다.
Theorem 2. Under Assumption 3 in the appendix, there exist constants $\left(C_0, C_1, C_2, C_3\right)$ independent of the stepsizes such that the convergence rate of our proposed cSGLD with cyclical stepsize sequence equation 1 is bounded for all $K$ satisfying $(K \bmod M=0)$, as $W_2\left(\mu_K, \nu_{\infty}\right) \leq$ \(C_3 \exp \left(-\frac{K \alpha_0}{2 C_4}\right)+\left(6+\frac{C_2 K \alpha_0}{2}\right)^{\frac{1}{2}}\left[\left(C_1 \frac{3 \alpha_0^2 K}{8}+\sigma C_0 \frac{K \alpha_0}{2}\right)^{\frac{1}{2}}+\left(C_1 \frac{3 \alpha_0^2 K}{16}+\sigma C_0 \frac{K \alpha_0}{4}\right)^{\frac{1}{4}}\right]\)
Particularly, if we further assume $\alpha_0=O\left(K^{-\beta}\right)$ for $\forall \beta>1, W_2\left(\mu_K, \nu_{\infty}\right) \leq C_3+$ $\left(6+\frac{C_2}{K^{\beta-1}}\right)^{\frac{1}{2}}\left[\left(\frac{2 C_1}{K^{2 \beta-1}}+\frac{2 C_0}{K^{\beta-1}}\right)^{\frac{1}{2}}+\left(\frac{C_1}{K^{2 \beta-1}}+\frac{C_0}{K^{\beta-1}}\right)^{\frac{1}{4}}\right]$.
여기서 그래서 $K \rightarrow \infty$로 보내면 결국 $W_2\left(\mu_K, \nu_{\infty}\right)$ 가 상수 $C_{3}$로 유계가 되는데 사실 이거도 잘 이해가 안되는데 저게 수렴하는걸 말하려면 0으로 수렴해야지 특정 상수로 유계가 되는걸 보여서 뭐 어쩌겠다는건지도 잘 이해가 되진 않는다. 물론 유계인거만해도 어느정도 잘 근사가 된다고 말할 순 있겠지만, 그게 weak convergence를 나타내냐? 라고 묻는다면 나는 잘 이해가 되지 않는다.
5. Experiment
원래는 실험파트가 조금 재미없어서 넘기는데 이 논문의 경우 실험 설정이 꽤나 재밌어서 가져와 봤다. 다양한 방법으로 실험해 해당 방법론의 유용함을 보였다. 특히 multi-modal 표본추출을 잘 하고 있다는 것을 보이기 위한 시도들이 조금 인상에 남은게 몇개 있어서 그것들 위주로 소개해 보려 한다.
5.1. Syntetic multimodal data
처음엔 시뮬레이션 상황에서 25개의 정규분포의 혼합분포로부터 표본추출을 하는 상황을 고려했다. SGLD와 cSGLD를 사용해 비교하였는데 SGLD는 4개의 마코프체인을 각각 50,000개의 길이로 표본추출 하였고, cSGLD는 50,000개 길이의 마코프체인을 단일로 추출하였다. 그때 결과는 다음과 같다.
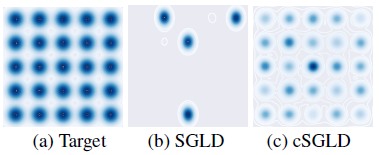
위에서 볼 수 있듯이 SGLD의 경우 4개의 마코프체인을 사용해 계산량이 많아졌음에도 25개중 4개의 mode밖에 찾아내지 못한 반면 cSGLD는 25개의 mode를 모두 찾아낸것을 확인가능하다.
5.2. Bayesian Neural Networks
이 다음 나온 실험상황은 cifar10과 cifar100 데이터에 대한 이미지 분류 딥러닝 모델에 적용하였다. 이때 모델 아키텍쳐로는 Resnet-18을 사용했고 200 에폭을 반복했다고 한다. 이때 결과는 다음과 같다.
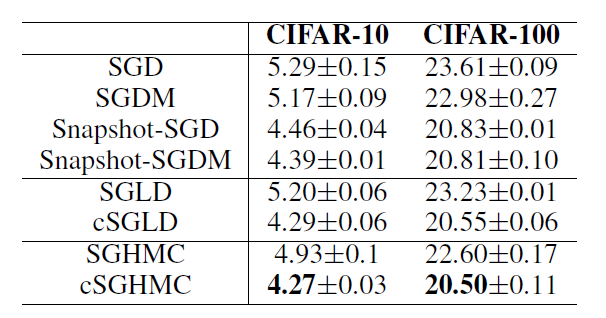

위의 표에서 보면 위에 표는 test error를 나타낸 표이고 아래 표 역시 test error을 나타냈다. 이 때 아래 표는 cifar100에서 체인의 개수를 다르게 하면서 실험한 결과이다. 위의 표를 보면 cSGMCMC가 다른 방법들보다 더 성능이 좋음을 확인가능했고 아래표에서 보면 Cyclical scheduler를 사용하고 단일 마코프체인을 사용할 경우 기존 방법론에 4개의 마코프체인을 사용한것보다 더 좋거나 혹은 비슷한 성능을 가짐을 확인 가능했다.
이렇게 단순히 test-error을 비교한것과는 달리 얼마나 multi-modal분포로 부터 표본을 잘 추출했는지 나타내는 실험 역시 진행하였는데 이게 좀 흥미로웠다.
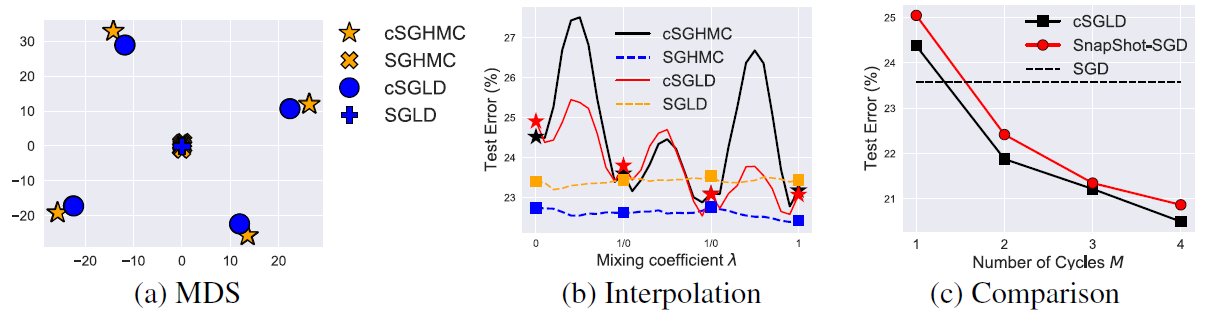
위 그래프에서 (a)는 각 방법론에서 추출된 표본을 군집분석한거로 대략 이해하면 좋을것 같다. 이 경우 SGLD와 SGHMC의 경우 하나의 군집만 나타났지만 cSGLD와 cSGHMC의 경우는 여러개의 군집이 나타나 multi-modal을 잘 나타낸것을 확인가능하다.
(b)역시 많이 흥미로웠는데, 이건 $\lambda \theta_1+(1-\lambda) \theta_2$, where $\lambda \in [0,1]$ 이로부터 test error을 계산한 것이다. 즉 표본된 추출이 있다면 그 중에 2개를 골라서 2개를 이은 선분 사이에 있는 점을 잡아서 test error을 계산한거로 볼 수 있다. 만약 한개의 mode로부터 표본들이 추출되었다면 저렇게 만든 값 역시 그 모드 주변에 있기 때문에 test error가 큰 변화가 없을 것이고 여러개의 mode로부터 표본이 추출되었다면 서로 다른 mode로부터 추출된 표본 사이의 $\theta$로 만든 test error은 기존것보다 더 커지면서 들쑥날쑥할거로 생각할 수 있다. 실제 결과를 보면 SGLD와 SGHMC의 경우 비교적 낮은값에서 smooth한 결과를 나타내지만 cSGHMC와 cSGLD의 경우는 보다 wiggly한 그래프로 나타내는것을 확인가능했다. 이를 통해 Cyclical scheduler를 사용하면 기존의 decreasing learning rate를 사용한거에 비해 multi-modal로부터 표본을 더 잘 추출함을 확인가능하다.
6. Summary
지금까지 확률적 몬테카를로 마코프체인에서 Cyclical scheduler를 적용한 cSGMCMC를 알아봤다. 실제 BNN을 적합할시에 local mode에 빠져서 문제가 생기는 경우가 많았는데 해당 방법을 적용해 이런 문제를 해결할 수 있을거로 생각된다. 또한 burn-in을 주기적으로 사용하는거도 흥미로운 내용이라고 생각되고, 또한 저런 실험 상황 설정 역시 앞으로 내가 논문을 쓰는데 있어서 참고 가능할거라 생각해 공부해봤다.
7. Reference
1. Zhang, Ruqi, et al. "Cyclical stochastic gradient MCMC for Bayesian deep learning." arXiv preprint arXiv:1902.03932 (2019).
댓글남기기