논문리뷰: Precondtioned Stochastic Gradient Langevin Dynamics for Deep Neural Networks?

목차

• Introduction
• Preliminaries
• pSGLD
• Summary

작년 8월달에 발 중족골 골절 수술 받으면서 발에 박아둔 철심을 뺀다고 2월 초에 또 수술하고 수술 후 관리한다고 그리고 설날이 있다는 핑계로 2월 내내 거의 공부를 하지 않았다. 원래 포스팅도 더 열심히 하고 다른 딥러닝 공부도 좀 많이 해두려 했는데 한 거 없이 2월이 다 지나가 버렸다. 그럼에도 다시 마음잡고 공부해야지. 그래서 오늘 살펴볼 논문은 이전에 공부했던 SGLD를 조금 수정시켜 발전한 방법론으로 이 역시 사후분포의 표본을 추출하는 알고리즘이다. 일반적인 SGD를 최적화할때 사용하는 방법론과 SGLD를 결합시킨 방법으로써 최적화 방법중 preconditioning을 SGLD에 적용시켰다해서 Precondtioned Stochastic Gradient Langevin Dynamics 줄여서 pSGLD라고 한다.

이번의 경우 논문 흐름을 따라가기 보단 내가 다시 재구성해서 작성해보려 한다.

1. Introduction

최적화 알고리즘에 있어서 gradient 앞에 학습률 $\epsilon_{t}$가 곱해지는데 이 경우 각 weight에 대해서 같은 값이 곱해지는 형태이다. 그런데 다음 상황을 생각해 보자.

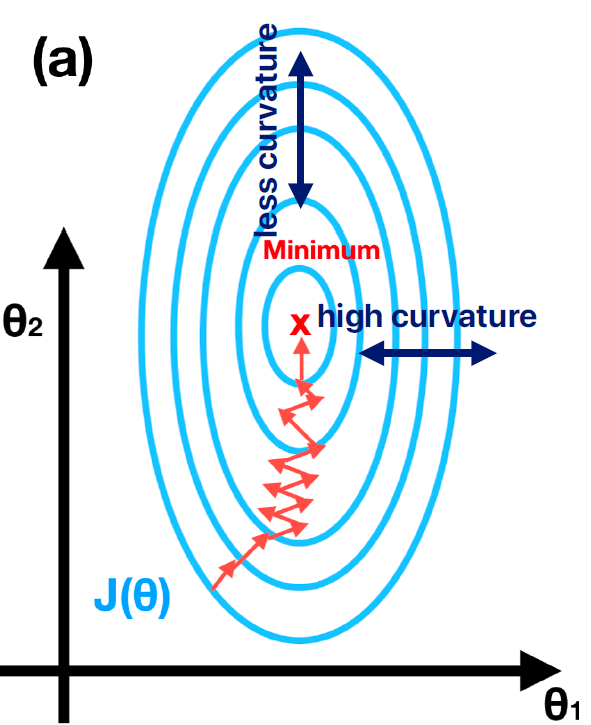
만약 weight $\theta_{1}$과 $\theta_{2}$에 대한 loss curvature가 다음과 같다면 두 weight를 학습시킬 때 같은 학습률을 사용하는것 보단 $\theta_{1}$에 대해서는 보다 큰 학습률을 사용하고 $\theta_{2}$에 대해서는 작은 학습률을 사용하는게 더 효율적일 것이다. 이제 이렇게 2차원인 경우가 아닌 딥러닝의 경우는 $\theta$의 차원수가 엄청 커지게 되는데 이런 경우 loss landscape는 훨씬 더 복잡해진다. 이런 문제를 해결하기 위해서 SGD에서는 normalization, momentum, preconditioning 등의 방법을 사용한다.

이제 이걸 일반적인 determinisic한 DNN이 아닌 bayesian neural network 상황에서 생각해보려 한다. 해당 논문은 이러한 문제를 SGLD와 preconditioning을 결합해 해결한다.

2. Preliminaries

본격적인 내용에 들어가기 전에 SGD에서 사용하는 precondintioning 알고리즘 중 하나인 RMSProp에 대해서 알아보자. 사실 정확한 precondintioning은 SGD에서도 잘 사용하지 않는다. 이게 weight의 차원이 커지면 precondintioning에 필요한 행렬의 헤이시안 행렬과 역행렬을 구하는거 자체도 연산량이 많이 필요해지기 때문에 scalable하지 않은 이슈가 있기 때문이다. 그래서 실제로는 대각행렬을 사용해 각 weight에 대해서 adaptive한 학습률을 곱하는 방법으로 최적화를 진행한다. 그 중에서 pSGLD와 관련된 RMSprop의 알고리즘은 다음과 같다.

위 알고리즘에서 보면 각 weight 앞에 동일한 학습률이 아닌 해당 weight의 index에 의존하는 값이 곱해진걸 확인 가능한다. 이 $r_{j}$ 보면 momentum의 형태로 이전 gradient의 제곱값을 누적시켜 얻은것을 확인 가능하다. 이런 형태를 SGLD에 적용시킨것이 pSGLD라 보면 될 것이다.

SGLD에 대한 설명은 이전 포스팅에서 하였으므로 해당 포스팅을 참고해 주면 될 것 같다. 한가지 주의해야 할 점은 SGLD와 마찬가지로 pSGLD에서도 학습률에 대한 2가지 가정(합이 발산, 제곱합이 수렴)이 성립해야지 수렴성이 보장된다.

3. pSGLD

위에서 언급한 것처럼 pSGDL는 RMSprop와 같은 preconditioners을 사용해 사후분포로부터 표본을 추출한다. 그러기 위해 각 반복 $t$에 대해 다음 값들을 정의한다.

\[\begin{aligned} & G\left(\boldsymbol{\theta}_{t+1}\right)=\operatorname{diag}\left(1 \oslash\left(\lambda 1+\sqrt{V\left(\theta_{t+1}\right)}\right)\right) \\ & V\left(\theta_{t+1}\right)=\alpha V\left(\boldsymbol{\theta}_t\right)+(1-\alpha) \bar{g}\left(\boldsymbol{\theta}_t ; \mathcal{D}^t\right) \odot \bar{g}\left(\boldsymbol{\theta}_t ; \mathcal{D}^t\right) \end{aligned}\]

여기서 몇 가지 기호와 식에 대해서 살펴보면, $\oslash$는 행렬에서 각 원소별로 나눗셈을 해주란 의미이고, $\odot$은 각 원소별로 곱하는 것을 의미한다. 그리고 $\alpha$는 위의 RMSprop 알고리즘에서 나온 decay rate $\rho$를 의미하고 이는 0과 1사이의 값이다. 마지막으로 \(\bar{g}\left(\boldsymbol{\theta}_t ; \mathcal{D}^t\right)=\frac{1}{n} \sum_{i=1}^n \nabla_{\boldsymbol{\theta}} \log p\left(d_{t_i} \mid \theta_t\right)\)

로 각 mini-batch안에서 gradient의 표본평균을 의미한다.

이 식을 보면 위에 나온 RMSprop의 알고리즘과 꽤나 유사함을 확인 가능하다. 보면 $V(\theta)$가 $r$의 역할을 하면서 $G(\theta)$에서 보면 $V(\theta)$에 제곱근을 씌어서 나눠주는데 이것이 $\frac{1}{\sqrt{r}}$의 역할을 한것으로 볼 수 있을 것이다.

이렇게 해서 계산한 $G(\theta_{t})$와 $V(\theta_{t})$를 사용해 사후분포로부터 $\theta_{t}$를 추출하는 알고리즘을 다음과 같이 제안한다.

위에서 $\Gamma(\theta)$가 새롭게 등장하는데 이는 $\Gamma_i(\boldsymbol{\theta})=\sum_j \frac{\partial G_{i, j}(\boldsymbol{\theta})}{\partial \theta_j}$ 이렇게 정의 된다. 이 경우 이것과 기존의 SGLD 알고리즘을 비교해보면 $\Delta \theta_{t}$에서 기존의 식에 $G(\theta_{t})$가 추가로 곱해지고 $\Gamma(\theta)$가 더해진걸로 볼 수 있다.

저자들은 Chen(2015)의 내용을 참고하고 변형해 해당 알고리즘이 수렴함을 보였다.

또한 그 뿐만 아니라 위 알고리즘에서 $\Delta \theta_{t}$가 생략되더라도 $O \left(\frac{(1 - \alpha)^{2}}{\alpha^{3}} \right)$ 만큼의 차이가 나 $\alpha$를 1과 가까히 했을때 사실산 큰차이가 나지 않아 $\Delta \theta_{t}$는 무시해도 됨을 보였다.

해당 내용에 대해 더 자세히 알고 싶은 사람은 이 논문의 appendix를 참고하면 좋을 것 같다.

4. Summary

저자들이 실험한 pSGLD와 SGLD의 Iterations 대비 Test error는 다음과 같다.

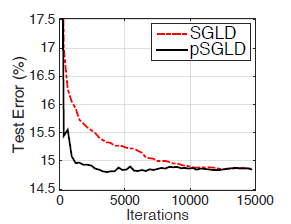
이를 보면 최종적인 test error는 동일하더라도 그 수렴속도에 있어서 pSGLD가 SGLD보다 훨씬 빠름을 확인 가능했다. 이는 SGD에서도 나타나는 현상으로 precondtioning해서 wiggly한 loss curvature를 잘 다룬것을 확인 가능했다.

그런데 여기서 한가지 의문점이 들었다. 저런 경우 DNN에서 또 많이 사용하는 방법이 batch normalization인데 이걸 BNN에 적용하면 어떨까 라는 생각이 들었다. 그래서 지금 실험코드를 짜서 batch norm+SGLD vs pSGLD를 해보려고 하는데 전자가 train cost나 train error은 잘 수렴하는데 test error에서 너무 불규칙하고 수렴하지 않아서 조금 더 연구해 봐야 겠다. 이런 연구가 많이 진행된 거 같진 않은데 만약 batch norm만 해도 된다면 굳이 $V(\theta)$를 계산할 필요가 없으니 더 빠르게 할 수 있지 않을까 생각이 드는데 잘 될지는 모르겠다.

5. Reference

1. Li, Chunyuan, et al. "Preconditioned stochastic gradient Langevin dynamics for deep neural networks." Proceedings of the AAAI conference on artificial intelligence. Vol. 30. No. 1. 2016.
2. Chen, Changyou, Nan Ding, and Lawrence Carin. "On the convergence of stochastic gradient MCMC algorithms with high-order integrators." Advances in neural information processing systems 28 (2015).