커널 방법 - 서포트벡터머신, 주성분분석에 활용

목차

• 동기
• 커널의 예시와 성질
  • 예시
  • 성질
  • 왜 작동하는가
  • 종류
  • 대표적인 커널의 종류
• 커널의 적용
  • 서포트벡터머신
  • 주성분분석
• 요약
• 참고자료

1. 동기

데이터 분석을 할 때 주어진 특성공간에서 데이터들의 특징을 파악하기 어려운 경우를 생각해보자.

혹은 서포트백터분류기 같은 선형 기법을 적용하려고 하지만, 주어진 특성공간에서 데이터들이 선형결정 경계로 분리되지 않는 경우를 생각해보자.

이럴 경우 주어진 특성공간을 더 높은 차원의 공간으로 변환하고, 그곳에서 데이터를 분석한 뒤에 다시 원래 공간으로 돌아오는 것을 생각 할 수 있다. 다음과 같은 상황이 그 대표적인 예시이다.

from IPython.display import Image
Image("idea.png", width=600)

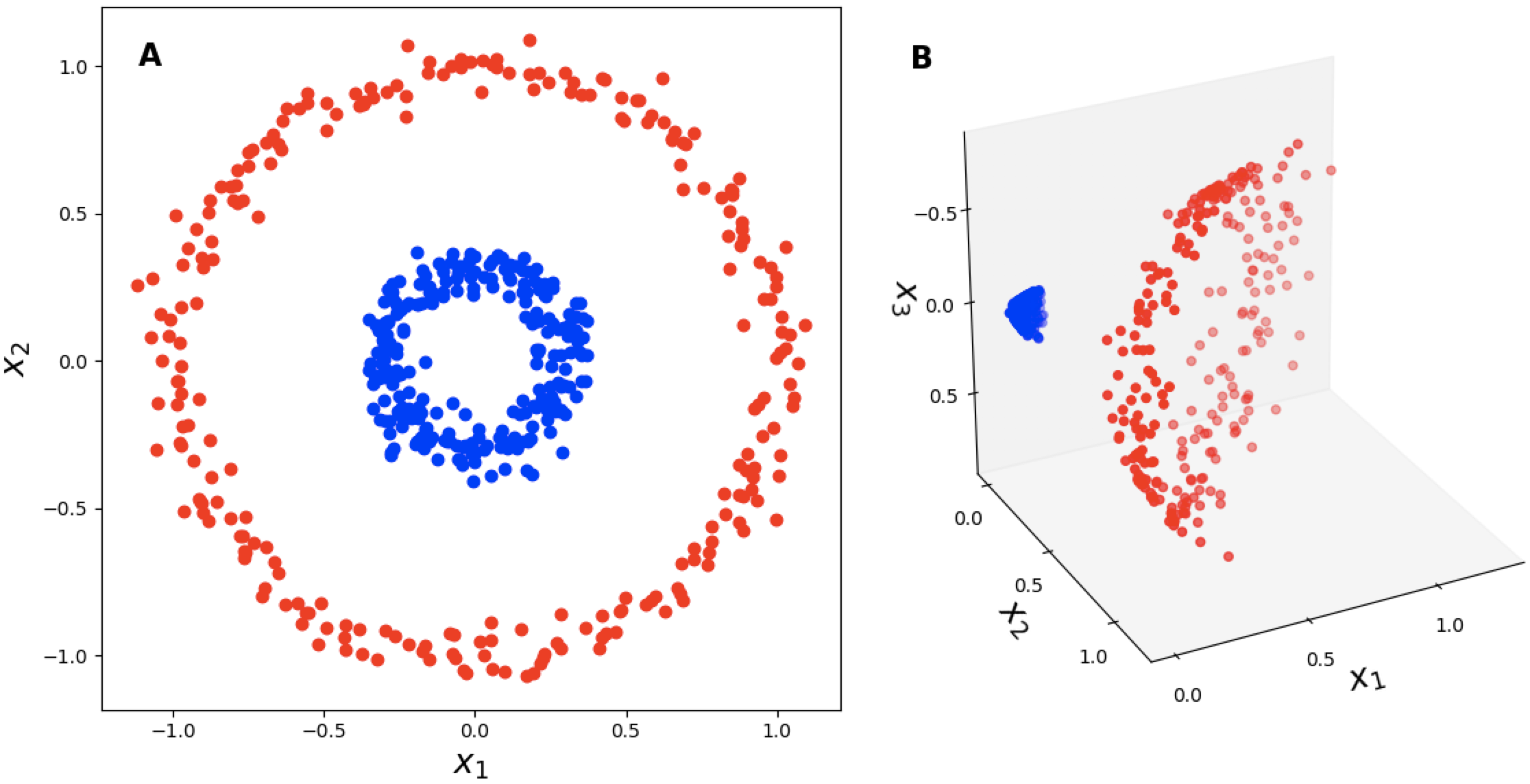
이 때, 원본공간 A에서 $X_1$과 $X_2$만 주어졌을 경우에는 주어진 데이터를 선형으로 분리할 수 없지만, 여기에 축을 하나 더 추가시킨 고차원 공간으로 변환해서 볼 경우에 주어진 데이터가 선형으로 분리됨을 볼 수 있다. 이런식으로 처음의 특성공간에서 잘 되지 않으니 뭔가 더 높은차원으로 옮겨가서 거기서 작업을 하자고 생각한게 커널방법의 가장 기본적인 동기이다.

그런데 여기서 문제가 발생한다. 저런식으로 고차원으로 변형하겠다는 생각을 한것은 좋지만, 그렇게 할 시에 계산량이 너무 많아지고 저장공간 또한 원래 상황에 비해서 기하급수적으로 많이 필요해 질 수 있다. 원래 처음특성공간이 2차원인데, 여기서 변환을 할 경우에 3차원 이상 더 높은 차원으로 변환하고 거기서 데이터 분석을 진행하기 때문에 저장공간과 계산측면에서 너무 비효율적일수 있다.

그래서 등장한것이 바로 커널(Kernel)이다. 직접적으로 데이터를 고차원 공간으로 변환시키는게 아닌 고차원에서 다뤘을때 나오는 그 결과물만 가저오겠다는 방법으로 이해하면된다.

조금 풀어서 설명하면, 보통 데이터를 다루는데 있어서 데이터 포인트들 사이의 유사도(similarity) 혹은 거리(distance)를 측정하기 위해서 두 표본사이의 내적(inner product), 즉 유클리드 공간에서는 소위 점곱(dot product)를 계산해야하는 경우가 많다. 하지만 여기서 $\phi(x)^{T} \phi(y)$ 를 직접 계산하는게 아닌(이때 $\phi()$는 저차원에서 고차원으로의 변환을 의미한다), $k(x,y) = \phi(x)^{T} \phi(y)$ 이렇게 되는 $k(x,y)$를 미리 생각해놓고 그냥 $k(x,y)$만을 계산해서 고차원 공간에서의 두 점사이의 유사도를 측정하겠단 것이다.

커널 방법의 기초적인 아이디어는 여기서 출발한다. 다음엔 이것에 대한 쉬운 예시를 살펴보도록 하자.

2. 커널의 예시와 성질

2.1. 커널의 예시

커널에 대한 기초적인 이해를 돕기 위해서 쉬운 예시를 생각해보자. 여기서 $\mathrm{R}^{2}$ 공간상에 두 점 $x, y$가 주어졌고 변환 $\phi : \mathrm{R}^{2} \rightarrow \mathrm{R}^{3}$이 다음과 같이 주어졌다고 하자.

\[\phi(x) = \phi((x_{1}, x_{2})) = (x_{1}^{2}, x_{2}^{2}, \sqrt{2}x_{1}x_{2})\]

이 경우 $\phi$는 2차원상의 점을 3차원으로 변환한다. 이 때 3차원상에서 두 점 사이의 유사도를 알기 위해선 점곱을 계산해한다. $\phi(x)$ 와 $\phi(y)$ 사이의 점곱을 구하면 다음과 같다.

\[\begin{aligned} \phi(x) \, \cdot \, \phi(y) & = (x_{1}^{2}, x_{2}^{2}, \sqrt{2}x_{1}x_{2}) \, \cdot \, (y_{1}^{2}, y_{2}^{2}, \sqrt{2}y_{1}y_{2}) \\ & = x_{1}^2 y_{1}^{2} + x_{2}^2 y_{2}^{2} + 2x_{1}x_{2}y_{1}y_{2} \\ & = (x_{1}x_{2} + y_{1}y_{2})^{2} = (x \, \cdot \, y)^{2} \end{aligned}\]

여기서 $k(x, y) = (x \, \cdot \, y)^{2}$로 정의를 해주는 것이다. 그렇다면 추후 저렇게 2차원 데이터를 3차원으로 변환해서 유사도를 구하고 싶을때 위와 같은 변환과정을 거치지 않고 바로 $k$만을 사용해서 고차원에서의 유사도를 구할수 있을것이다.

이렇게하면 각 데이터와 새로운 데이터에 대해서 $\phi(x)$를 직접 계산할 필요가 전혀 없어지니 연산속도와 저장공간 측면에서 엄청난 이점이 생기고, 그와 동시에 저차원을 고차원으로 옮겨서 선형경계를 찾는것과 같은 작업을 하게 해준다.

2.2. 커널의 성질

커널이 학습과정에서 유의미하게 사용되려면 아무것이나 사용한다고 되는게 아니라 크게 두가지 성질을 만족해야 한다.

1. 커널은 반드시 대칭적(symmetric)이어야한다. 즉 $k(x, y) = k(y, x)$ 를 모든 $x, y$에 대해서 만족해야 한다.
2. 커널은 반드시 반양정치(positive semi definite)이어야 한다. 즉,

\[\forall c_i \in \mathrm{R}, x_{i} \in \Omega, \qquad \sum_{i}^{n} \sum_{j}^{n} c_{i}c_{j}k(x_{i}, x_{j}) \geq 0\]

1. 또한 대부분의 경우 $k(x, y) \geq 0$ 이 성립한다.

여기서 커널을 스케일링해서 $k(x, y) = 1 \Leftrightarrow x =y$ 가 되도록 해주는 경우도 있다.

이것을 의미를 살펴보면 커널은 두 데이터간의 유사도를 측정하는 단위이다. 이때 그 유사도는 0에서 1사이에서 움직이며 1일때가 유사도가 최대로서 두 데이터가 일치하는 경우이고 0일때가 두 점사이의 유사도가 제일 떨어지는 경우로 받아드리면 될 것 같다. 또한 유사도를 측정하는것이므로 x와 y의 유사도를 측정하는것이나 y와 x의 유사도를 측정하는 것이나 동일해야 잘 정의됨을 자명할 것이다.

2번째 조건에 대해서는 다음의 정리를 참고하면 좋을것 같다. 일반적으로 사용하는 입장에서는 중요하지 않을 수 있으나 통계적으로는 중요한 정리이니 한번 보고가도록 하자.

2.3. 커널이 왜 작동하는가

정리 : $k: \Omega \times \Omega \rightarrow \mathrm{R}$ 이 반양정치(positive semi definite, p.s.d) 커널이라 하자. 그러면 재생 커널 힐베르트 공간(RKHS, Reproducing Kernel Hilbert Space) $\mathrm{H}$과 변환 $\phi : \Omega \rightarrow \mathrm{H}$가 존재해서 다음을 만족한다.

\[\forall x,y \in \Omega, \quad k(x, y) = \phi(x) \cdot \phi(y)\]

이 때, 힐베르트 공간(Hilbert Space)는 내적(inner product)이 정의된 완비노름공간(complete normed space)이다.

이 정리에 대한 자세한 내용은 이 포스팅의 내용을 훨씬 뛰어넘으므로 간략하게만 살펴보도록 하자.

일단 힐베르트 공간은 소위 “좋은 공간”으로 받아드리도록 하자. 노름이 정의되서 크기와 거리를 잴 수 있으며 완비성을 만족해 수렴할 수 있고 내적까지 정의된 공간으로 볼 수 있다. 쉬운 예시로 일반적인 유한차원 유클리드 공간같은걸 생각하면 될 것이다.

그렇다면 커널이 반양정치라면 어떤 변환이 존재해서 그 변환이 원래 주어진 특성공간을 좋은 힐베르트 공간으로 변환시킬 수 있고 거기서의 내적이 원래의 커널과 같다는 말이니 쉽게 말해서 커널이 잘 정의가 된다는 말이다. 그래서 우리가 커널만을 사용해서 고차원에서 데이터분석을 한 것 마냥 비선형 문제를 다룰 수 있는 것이다.

여기서 그러면 커널이 반양정치여야하는 건 알겠다고 하자. 그러면 잘 알려진 커널이 아닌 새로운 커널을 만들거나 낯선 커널을 만났을 때 어떻게 하면 그것이 반양정치인것을 보일 수 있을까?

일단 그것을 수학적으로 증명하는 법도 있겠지만 우리는 시뮬레이션 데이터 포인트에 대해서 커널 행렬(kermatrix) $\mathrm{K}$를 만들어서 이 행렬이 반양정치행렬인지 확인하도록 하자. 즉 시뮬레이션 데이터 포인트 $x_{i}, x_{j}$에 대해서 $\mathrm{K}_{ij} = k(x_i, x_j)$라 할때 nxn행렬 K가 양반정치행렬이 되는지 확인하면 된다.

2.4. 대표적인 커널의 종류

다음으로 넘어가기 전에 자주 사용하는 대표적인 커널 몇개만 확인하고 가도록 하자.

1. 다항커널

\[k(x_{i}, x_{j}) = (x_{i} \cdot x_{j} + \theta)^{p}\]

1. 하이퍼볼릭 탄젠트(hyperbolic tanget) 혹은 시그모이드(sigmoid) 커널

\[k(x_{i}, x_{j}) = \mathrm{tanh}(\eta (x_{i} \cdot x_{j}) + \theta)\]

1. 방사 기저 함수(Radial Basis Function, RBF) 또는 가우시안 커널

\[k(x_{i}, x_{j}) = \mathrm{exp}\left(-\frac{\|x_{i}-x_{j}\|^{2}}{2\sigma^{2}} \right)\]

혹은

\[k(x_{i}, x_{j}) = \mathrm{exp}\left(-\gamma\|x_{i}-x_{j}\|^{2} \right)\]

이 경우 각 식에 있는 하이퍼파라메터(hyperparameter)는 데이터에 맞춰서 적절히 튜닝되어야 한다. 주로 교차검증(cross validation)을 사용한다.

3. 커널의 활용

지금까지 커널에 대해서 기본적인 내용을 살펴봤다. 그러면 커널이 학습에 어떻게 적용될 수 있는지에 대해서 살펴보록하자. 커널은 가장 기본적인 선형회귀부터 RKHS를 사용해 조건부독립을 확인하는 등 매우 다양한 영역에서 사용될 수 있지만 여기서는 그중 가장 유명한 서포트벡터머신(SVM)과 주성분분석(PCA)를 위주로 알아보도록하자.

3.1. 서포트벡터머신(Support vector machine, SVM)

서포트벡터분류기(Support vector classifier)는 주어진 데이터들을 분류하는데 분리초평면을 사용해서 마진이 가장 크도록 해준다. 이때 분리초평면을 사용하기 때문에 서포트벡터분류기는 선형결정경계를 가지게되서 비선형 데이터를 다루기 어려운 단점이 있다.

그러나 여기서는 자세한 식을 다루지는 않겠지만 분리초평면을 구하는 식과, 그것의 최적화 함수를 보면 결국엔 데이터들 간의 점곱으로 표현됨을 유도할 수 있다. 이 점곱의 형태를 커널로 바꿔저서 선형인 분류기를 비선형 분류기로 바꿔준게 서포트벡터머신이라 보면 될 것 같다.

이 포스팅에서는 자세한 식은 생략하고 예제와 사이킷런을 통한 구현을 알아보도록 하자.

import matplotlib.pyplot as plt
import numpy as np
np.random.seed(1)
X_sor = np.random.randn(200, 2)
y_sor = np.logical_xor(X_sor[:, 0] > 0,
                       X_sor[:, 1] > 0)
y_sor = np.where(y_sor, 1, -1)
plt.scatter(X_sor[y_sor == 1, 0],
            X_sor[y_sor == 1, 1],
            c = 'b', marker = 'x', label = '1')
plt.scatter(X_sor[y_sor == -1, 0],
            X_sor[y_sor == -1, 1],
            c = 'r', marker = 's', label = '-1')
plt.xlim([-3, 3])
plt.ylim([-3, 3])
plt.legend(loc = 'best')
plt.show()

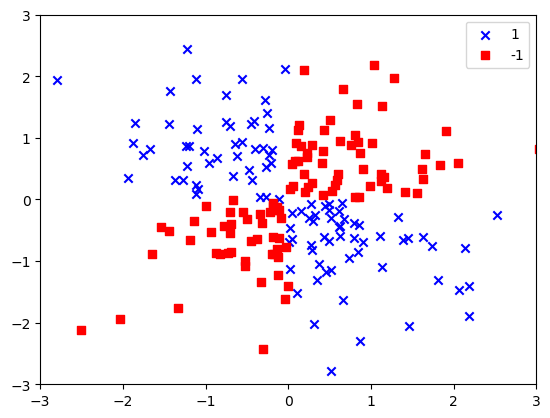
여기서 랜덤하게 노이즈가 섞인 200개의 2차원 데이터셋을 만들었다. 보면 확실히 두 클래스를 선형 결정경계로 분리 할 수 없음을 확인 할 수 있다. 이렇게 선형으로 분리되지 않는 경우 비선형분리를 하기 위해서 커널 서포트벡터머신이 사용될 수 있다. 위에서 언급한 3가지의 커널중 방사 기저 함수를 사용해보도록 하자

from sklearn.svm import SVC
from mlxtend.plotting import plot_decision_regions
svm = SVC(kernel='rbf', random_state=1, gamma=0.1, C=1.0)
svm.fit(X_sor, y_sor)
plot_decision_regions(X_sor, y_sor, clf=svm)
plt.xlim([-3, 3])
plt.ylim([-3, 3])
plt.legend(loc='upper left')
plt.show()

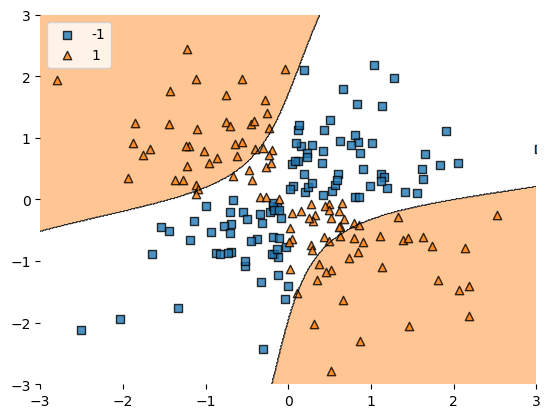
이로부터 방사기저커널을 사용한 서포트벡터머신이 비선형 결정경계를 찾을 수 있음을 확인할 수 있다.

이때 gamma값과 규제강도 C를 적절히 튜닝하면 더 좋은 결과를 얻을 수 있을 것이다. 위에서도 말한것 처럼 주로 교차검증을 사용하지만 여기서는 다루지 않고 다음에 다루도록 하겠다.

3.2. 주성분분석(Principal component analysis, PCA)

위의 경우인 서포트벡터머신은 타겟 레이블(target label)이 주어진 지도학습(supervised learning)의 한 종류이다. 이번에는 타겟 레이블이 주어지지 않은 상황에서 차원축소(dimension reduction)을 수행하는 PCA에 커널을 적용하는 것을 알아보도록 하자.

일반적인 PCA의 경우 주어진 데이터 행렬 X에 대해 공분산 행렬 X에 대한 주성분을 뽑아내고 그 주성분에 각각의 데이터를 사영시켜 차원축소를 진행한다. 이 때 주성분은 모든것을 사용하는게 아닌 자료의 정보를 많이 가지고 있는 즉 데이터 방향에서 분산이 큰 몇개의 축만을 골라서 사용한다.

마찬가지로 커널주성분분석(Kernel Principal component analysis, KPCA) 역시 $\phi(X)$에 대해 주성분분석을 진행하는것으로 생각하면 좋을것같다. 그러나 이 역시 이전에 설명한것과 서포트 벡터머신의 경우처럼 $\phi(X)$을 직접 사용하는것이 아니라 커널을 사용해서 주성분 분석을 진행한다.

이 때 주성분 분석과 커널방법을 적절히 잘 사용하면 결국 이는 $\mathrm{K} = \phi(X)\phi(X)^{t}$ 를 구하면 되는 문제로 바뀜을 알 수 있다. 이에 대한 자세한 내용은 여기서는 생략하도록 하겠다. 저 커널행렬 $\mathrm{K}$는 2.3.절에 나온것과 동일하게 주어진 데이터 포인트에 대해서 정의될 수 있다.

그러한 방식으로 커널 행렬 $\mathrm{K}$를 구했으면 이것의 고유벡터 중 해당하는 고유값이 큰 최상위 벡터 몇개를 적당히 고르면 그것이 찾고자 한 차원축소된 데이터셋이 된다.

여기서 주의할 것은 일반적인 PCA에서는 고유벡터를 구하면 그것과 데이터 사이의 점곱을 구해서 사영을 시켜야 했지만 이 경우에는 K의 고유벡터 자체가 이미 주성분 축에 사영된 데이터임을 명심하자.

이 역시 예제를 통해서 확인해보도록 하자.

from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, random_state=123)
plt.scatter(X[y==0, 0], X[y==0, 1],
            color = 'red', marker = '^', alpha=0.5)
plt.scatter(X[y==1, 0], X[y==1, 1],
            color = 'blue', marker = 'o', alpha=0.5)
plt.show()

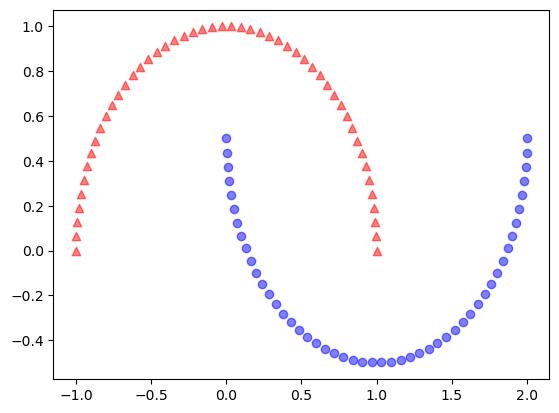
이 경우 반달 모양의 2차원 데이터셋을 생성하였다. 산점도에서 확인 할 수 있듯이 이 데이터셋은 선형결정경계로 분리되기는 어려워 보인다. 또한 여기서 시각적으로 확인하기 위해서 색과 모양을 줬지만 실제로는 레이블이 되있지 않다고 생각해야 한다. 이 경우 먼저 일반적인 PCA를 적용해서 주성분에 투영해보도록 하자.

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
fig, ax = plt.subplots(nrows = 1, ncols =2, figsize = (7, 3))
ax[0].scatter(X_pca[y==0, 0], X_pca[y==0 , 1],
              color='red', marker = '^', alpha = 0.5)
ax[0].scatter(X_pca[y==1, 0], X_pca[y==1 , 1],
              color='blue', marker = 'o', alpha = 0.5)
ax[1].scatter(X_pca[y==0, 0], np.zeros((50, 1)) + 0.02,
              color='red', marker = '^', alpha = 0.5)
ax[1].scatter(X_pca[y==1, 0], np.zeros((50, 1)) - 0.02,
              color='blue', marker = 'o', alpha = 0.5)
ax[0].set_xlabel("PC1")
ax[0].set_xlabel("PC2")
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel("PC1")
plt.show()

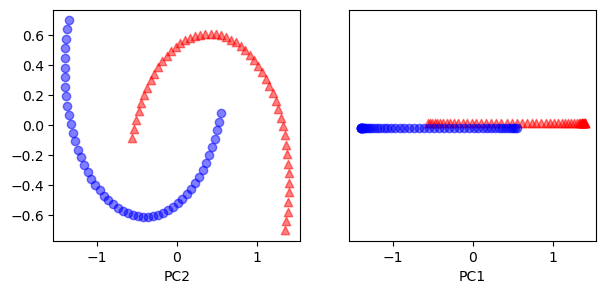
이 결과에서 일반적인 PCA로부터는 차원축소를 해서 유의미한 분석을 하기 어렵다고 판단할 수 있다.

이번에는 커널 PCA를 적용해 보도록 하자. 이 경우역시 동일한 데이터셋에 방사 기저 함수를 사용한 주성분 분석을 적용해 보도록 하자.

from sklearn.decomposition import KernelPCA
X, y = make_moons(n_samples=100, random_state=123)
kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)
X_kpca = kpca.fit_transform(X)
fig, ax = plt.subplots(nrows = 1, ncols =2, figsize = (7, 3))
ax[0].scatter(X_kpca[y==0, 0], X_kpca[y==0 , 1],
              color='red', marker = '^', alpha = 0.5)
ax[0].scatter(X_kpca[y==1, 0], X_kpca[y==1 , 1],
              color='blue', marker = 'o', alpha = 0.5)
ax[1].scatter(X_kpca[y==0, 0], np.zeros((50, 1)) + 0.02,
              color='red', marker = '^', alpha = 0.5)
ax[1].scatter(X_kpca[y==1, 0], np.zeros((50, 1)) - 0.02,
              color='blue', marker = 'o', alpha = 0.5)
ax[0].set_xlabel("PC1")
ax[0].set_xlabel("PC2")
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel("PC1")
plt.show()

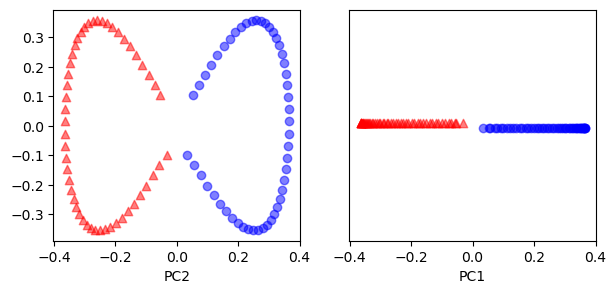
이 경우에는 주성분 축 하나만 사용하더라도 주어진 데이터를 잘 구분할 수 있는걸 확인할 수 있었다.

이런식으로 주성분분석에도 커널을 적용해서 차원축소를 진행할 수 있다.

여기서는 실제로는 레이블이 주어지지 않아 분류를 할 수는 없지만, 저렇게 주성분 분석을 진행하고 나면 저것을 통해 군집분석(clustering) 혹은 시각화 등을 효율적으로 진행할 수 있을것이다.

요약

지금까지 커널 방법의 동기와 그 성질 그리고 적용될 수 있는 간단한 학습기법들에 대해서 살펴보았다.

앞에서도 얘기한것처럼 커널은 고차원 분석을 저차원에서 실행시켜주는것으로 실제로 컴퓨터 하드웨어가 많이 발달하지 못했던 1990년대 혹은 2000년대 초반에 유행했던 방식이라고 한다. 실제로 다층신경망의 개념 자체는 1960년대에도 있었다고하나 그때는 컴퓨팅 능력의 한계로 신경망같은 복잡한 비선형모형은 꿈에도 꾸지 못했고, 그때만 해도 이런 커널을 사용한 서포트벡터머신이 완전히 신경망을 앞서고 있던 시대였다고 한다.

그러나 시대가 발전함에 따라 컴퓨팅 자원이 늘어나고 데이터의 수도 기하급수적으로 많아짐에 따라 지금 와서는 신경망 딥러닝 모델이 대세가 되어버렸지만서도 저런 커널의 아이디어나 적용방법 등은 아직도 유효하다고 생각해 이렇게 정리를 해 보았다.

참고자료

1. Hastie, Tibshirani, Friedman, Tibshirani, Robert, Friedman, J. H., and SpringerLink. The Elements of Statistical Learning : Data Mining, Inference, and Prediction / Trevor Hastie, Robert Tibshirani, Jerome Friedman. (2009). Print.

2. Raschka, Mirjalili, 박해선, and Mirjalili, Vahid. 머신 러닝 교과서 with 파이썬, 사이킷런, 텐서플로 / 세바스찬 라시카, 바히드 미자리리 지음 ; 박해선 옮김 (2019). Print.