Dimensionality Reduction for visualization using t-SNE

목차

• 동기
• 차원 축소 방법의 종류
  • Projection(사영)
  • Manifold Learning(다양체 학습)
• SNE(Stochastic Neihbor Embedding)
  • 아이디어
  • 작동원리
  • 문제점
• t-SNE(t-distribution Stochastic Neihbor Embedding)
  • 아이디어
  • 작동원리
  • 주의사항
• 예시 코드
• 결론
• 참고자료

1. 동기

이번 포스팅에서는 이전 interpretability에 관한 포스팅에서 언급한 내용 중 하나인 t-SNE에 대해서 알아보려고 한다. t-SNE는 PCA와 유사하게 고차원의 데이터에서 차원 축소를 통해서 시각화를 하는 unsupervised learning의 일종이다. t-SNE의 창시자중 한명인 Laurens Van Der Maaten의 말을 빌리면

“Always visualize your data first, before you start to train predictors on the data! Oftentimes, visualizations such as the ones I made provide insights into the data distribution that may help you in determining what types of prediction models to try.”

즉, 데이터 시각화는 주어진 데이터 모델의 분포와 어떤 예측모델을 사용해야 할지에 대한 통찰을 제공해 줄 수 있기 때문에 이를 모델링 하기 전 항상 먼저 적용해 보라고 말한다.

또한 이전 포스팅에서 설명한것 처럼 t-SNE는 딥러닝 모델을 해석하는 과정에서도 사용될 수 있는데, 마지막 hidden layer의 feature들에 대해서 적용해서 모델을 분석할 수 있다고 한다.

이에 대해서는 해당 웹사이트(https://learnopencv.com/t-sne-for-feature-visualization/)를 참고해주면 좋을 것 같다.

이 처럼 데이터 시각화는 필수적인 과정이고 이를 시행할 때 고차원의 정보(information)를 최대한 잃지 않으면서 저차원으로 나타내는게 중요하다. 이 때 정보(information)는 데이터들끼리의 neigborhoodness,similiarity, dissimilarity를 의미한다.

2. 차원 축소 방법의 종류

본격적으로 내용에 들어가기전 여러 차원 축소 방법의 서로 다른 접근 방식과 그 차이에 대해서 간단히 알아보자.

2.1. Projection(사영): 고차원 데이터를 저차원 공간으로 사영시켜서 차원 축소를 하는 방법

• 선형 방법이다
• PCA(Principle component analysis, 주성분분석), LDA(Linear Discriminant Analysis, 선형판별분석), PLS(Partial Least Squares, 부분최소제곱법)

이 경우 PCA는 데이터들의 분산이 가장 큰 축과 그에 수직이 되는 축을 이용해서 저차원으로 사영하는 방법이다. PLS 여기서 설명된 다른 방법들과 달리 주로 regression문제에서 사용되는 차원축소방법으로 PCR을 target variable을 사용해서 보완한 방법이다. 이들 방법 또한 많이 사용되는 방법이지만, 사용되는 축들을 제외한 나머지 축들을 무시하기 때문에 그에 대한 정보를 잃어버리는 경우가 생긴다.

from IPython.display import Image
Image("PCA.png", width=600)

2.2. Manifold Learning(다양체 학습) : 훈련 데이터가 놓여져있는 다양체를 학습하는 방법

• 비선형 방법이다
• SNE(Stochastic Neihbor Embedding), t-SNE(t-distribution Stochastic Neihbor Embedding), UMAP(Uniform Manifold Approximation and Projection)

Manifold란 위상수학에 나오는 개념인데, 대략 어떤 각각의 점 주변에서 보면 유클리드 공간과 비슷하게 생각할 수 있는 위상공간으로 이해하면 좋을것 같다. 즉, Manifold learning은 주어진 고차원 훈련데이터에 대해서 원래 점들의 이웃, 유사성 혹은 비유사성을 최대한 보존하는 저차원 다양체를 학습하는 비지도학습이다.

우리는 이번 포스팅에서는 SNE와 t-SNE에 초점을 맞출것이며, 이들은 local structure을 보존하며 최대한 original neighborhood를 보존하는 Low dimensional space를 학습하는게 목적이다.

또한 변수선택에 사용되서 추후 회귀나 분류모델의 전작업으로도 사용될 수 있는 PCA와 달리 이들 방법은 데이터에 왜곡이 있을수 있기 때문에 오직 시각화에만 사용되어야 한다.

Image("tsne.png", width=600)

3. SNE(Stochastic Neighbor Embedding)

3.1. 아이디어

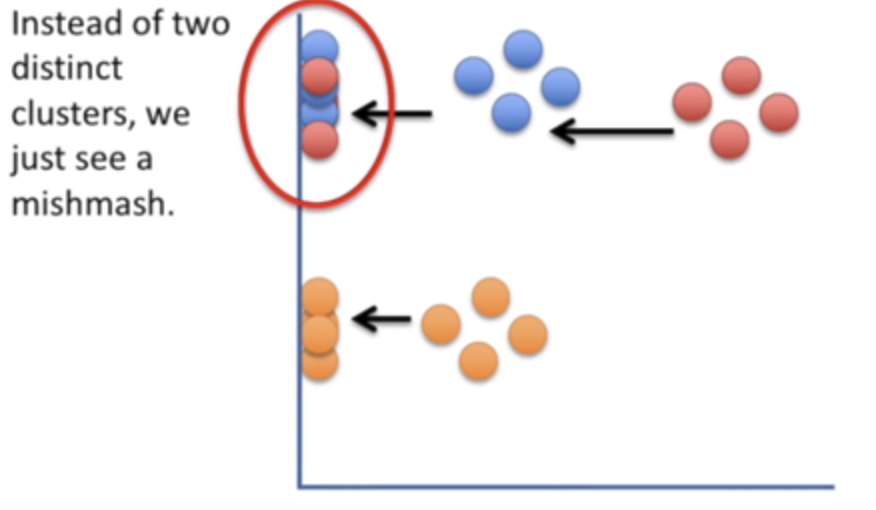
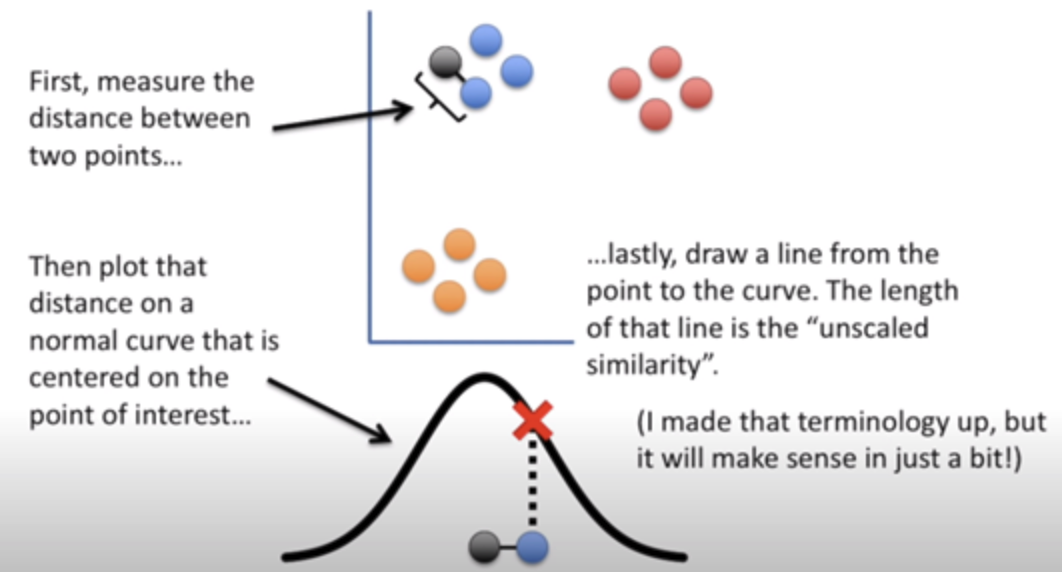
원래 데이터에서 한 점($x_{i}$)을 중심으로, 다른 점($x_{j}$) 사이의 거리를 측정해 확률분포 $P$로 만들고 그것과 훈련해야할 저차원 공간 $y_{i}$ 와 $y_{j}$사이의 거리를 축정해 만든 확률분포 $Q$ 이 두 분포를 유사하게 만들어 줌으로써 저차원 공간을 학습해 나가는 방법이다.

이 때 $x_{i}$과 $x_{j}$ 사이의 거리를 측정할 때 $x_{i}$를 중심으로 한 정규분포(혹은 방사기저 커널)을 사용하고 마찬가지로 $y_{i}$와 $y_{j}$사이의 거리를 측정할 때도 방사기저 커널을 사용해서 측정한다. 또한 그렇게 만든 $P$와 $Q$가지고 KL divergence(Kullback-Leibler divergence)를 사용해서 분포 사이간의 거리를 측정하는 손실함수를 만들고 이를 경사하강법을 통해서 최소화하는 방법으로 저차원 공간을 학습해 간다.

3.2. 작동원리

$i \rightarrow j$ 즉 $x_{i}$를 기준으로한 $x_{j}$의 거리(확률)은 다음과 같이 정의된다.

\[p_{j|i} = \frac{exp(-\|x^{(i)} - x^{(j)}\|^{2}/2\sigma_{i}^{2})}{\sum_{k \neq i}{exp(-\|x^{(i)} - x^{(k)}\|^{2}/2\sigma_{i}^{2})}}\]

또한 이경우,

\(p_{i|i}=0\) 으로 정의한다.

이 때,

\(p_{j|i} \neq p_{i|j}\) 이고 분산 $\sigma_{i}^{2}$ 이 각 i마다 다르다는것에 주의해야 한다.

이에 대해서,

\(P_{ij} = \frac{1}{2N}(P_{j|i} + P_{i|j})\) 로 정의해 최종적인 분포가 symmetric이 되도록 해주는 경우도 있다.

$\sigma_{i}^{2}$은 각 data point를 기준으로 얼만큼 많은 점들을 neighborhood로 취급할 건지를 결정해 준다고 이해할 수 있다. 예컨데 $\sigma_{i}^{2}$이 크면 정규본포는 거의 평평하게 되기 때문에 모든 점들을 neighborhood로써 취급하지만 $\sigma_{i}^{2}$이 작으면 $x_{i}$를 중심으로 분포가 몰려있기때문에 $x_{i}$와 정말 가까운것에만 확률값(거리)를 주고 나머지는 0으로 만드는 효과가 있다. KNN에서 k-parameter역할을 비슷하게 수행한다고 이해할 수 있다.

이때 $\sigma_{i}^{2}$에 대한 parameter는 perplexity로 구현되어 있다.

\[perplexity(P_{.|i} = 2^{H(P_{.|i})})\]

로 정의 되며,

\(H(P_{.|i}) = -\sum_{j} P_{j|i}\log_{2}{(P_{j|i})}\) 은 entropy를 의미한다. 이 때 perplexity와 $\sigma_{i}^{2}$는 대략 비례하는 관계를 가지고 있다. 즉 perplexity가 작으면 $x_{i}$ 주변의 적은 점만 이웃으로 취급하지만 perplexity가 크면 더 많은 점들을 이웃으로 취급하는 경향이 있다.

Image("sne1.png", height=100)

이와 마찬가지로 저차원 공간에서도 분포(유사도)를 정의해 줄 수 있다. 이는 다음과 같이 정의된다.

\[q_{j|i} = \frac{exp(-\|y^{(i)} - y^{(j)}\|^{2})}{\sum_{k \neq i}{exp(-\|y^{(i)} - y^{(k)}\|^{2})}}\]

이 경우는 \(p_{j|i}\) 와 달리 $\sigma_{i}^{2}$ 으로 나눠주지 않음에 주의해야 한다. 이렇게 만든 $P$와 $Q$를 사용해 이 분포들의 유사도를 측정해 그것을 이 unsupervised learning의 loss function으로 삼아 경사하강법을 통해줄여가면서 학습해가는게 핵심 원리이다. KL divergence를 사용한 loss function은 다음과 같이 정의된다.

\[C = \sum_{i}{KL(P_{i}\|Q_{i})} = \sum_{i}\sum_{j}{p_{j|i}\log{\frac{p_{j|i}}{q_{j|i}}}}\]

이때 이는,

\(\sum_{i}\sum_{j}{p_{j|i}\log{\frac{p_{j|i}}{q_{j|i}}}} = - \sum_{ij}{P_{i|j}\log(Q_{i|j})} + K\) (단, K는 상수)가 된다.

이 때 이것의 ($y_{i}$에 대한)gradient는 정말 간단하게 표현이 된다.

\[\frac{\partial C}{\partial y_{i}} = 2 \sum_{j \neq i}{(p_{j|i} - q_{j|i} + p_{i|j} - q_{i|j})(y_{i} - y_{j})}\]

위의 gradient를 사용해 $y_{i}$ 들을 각 epoch마다 update해주는 방식으로 학습이 진행된다. 또한 각 차원마다 학습률(learning rate)를 다르게 하기위해서 momentum term을 더해서 최적화를 진행한다.

이에 대해서 생각해보면 $P$와 $Q$의 차이가 큰 경우 \(p_{j|i} - q_{j|i} + p_{i|j} - q_{i|j}\) 값이 큰 양수가 되서 이게 $y_{i}$ 에 대해서 빼지니까 $y_{i}$ 가 $y_{j}$ 로 부터 떨어져있을때 더 가깝게 끌어오는 효과를 낸다고 이해할수 있을것같다.

Image("sne2.png", width=600)

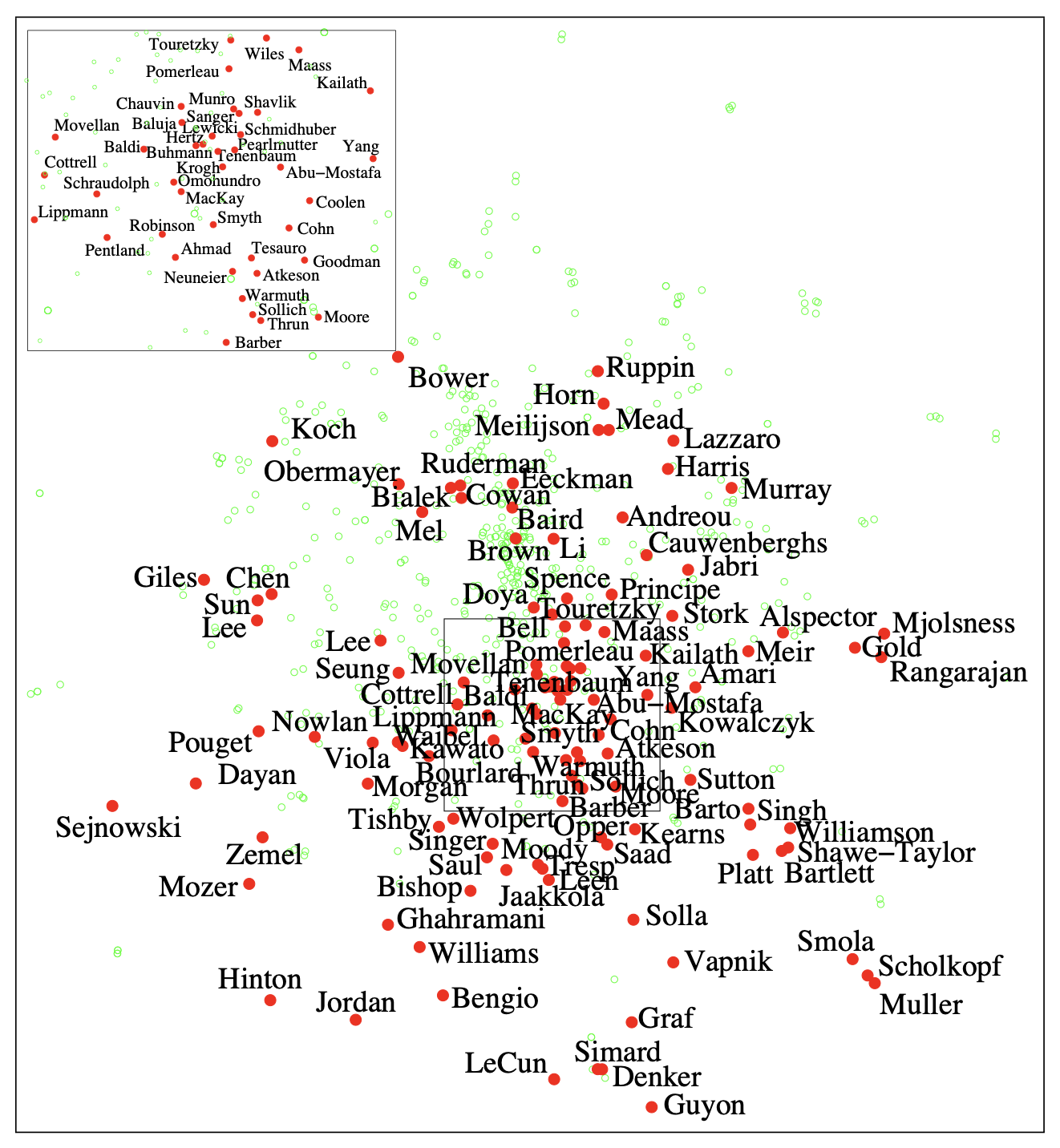
3.3. 문제점

위의 경우는 서로 cowork한 교수님들을 t-SNE를 통해서 시각화한것인데 보다싶이 너무 몰려있어서 잘 구분이 되지 않는 경향이 있다.이와 같이 고차원에서 넓게 넓게 퍼져있던 데이터 셋들을 저차원으로 줄여버리면 필연적으로 더 붙어있을수밖에 없는 현상이 발생하는데 이걸 “crowding problem”이라고 한다. 해당 논문에서는 고차원에서는 많은 방들이 있지만 저차원에서는 방의 수가 줄어서 더 붙어있다고 비유를 든다. 이것은 SNE의 가장 큰 문제점 중에 하나이며, $Q$의 분포를 구하는데 있어서 보다 꼬리가 두꺼운 t-distribution을 사용해서 문제를 해결하려고 시도한다.

4. t-SNE(t-distribution Stochastic Neighbor Embedding)

4.1. 아이디어

위와 같은 SNE의 crowding 문제를 해결하기 위해서 $Q$, 즉 저차원의 분포를 구할 때 정규분포가 아닌 t-분포를 사용하는것이 t-SNE이다. 왜 t-분포를 사용하는지 직관적으로 이해하기 위해서 일단 t-분포와 정규분포의 차이를 해당 분포의 그래프로 확인해보도록 하자.

Image("tdist.png", width=600)

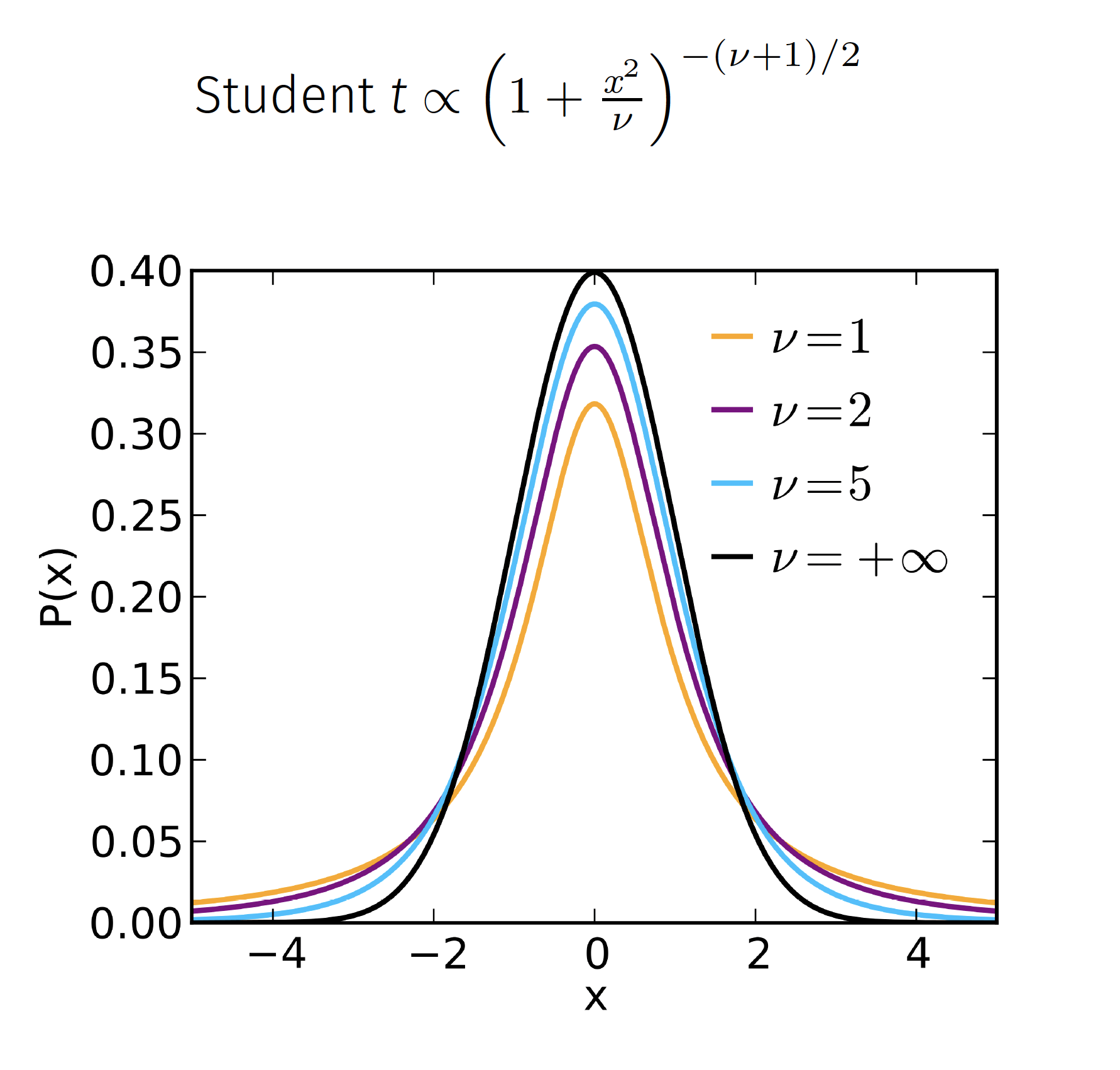
위의 그림에서 볼 수 있듯이, t-분포는 정규분포에 비해서 그 꼬리가 더 두껍게 나오는것을 알 수 있다. 이에 따라서 다음과 같은 경우들이 발생한다.

Image("tsne1.png", width=600)

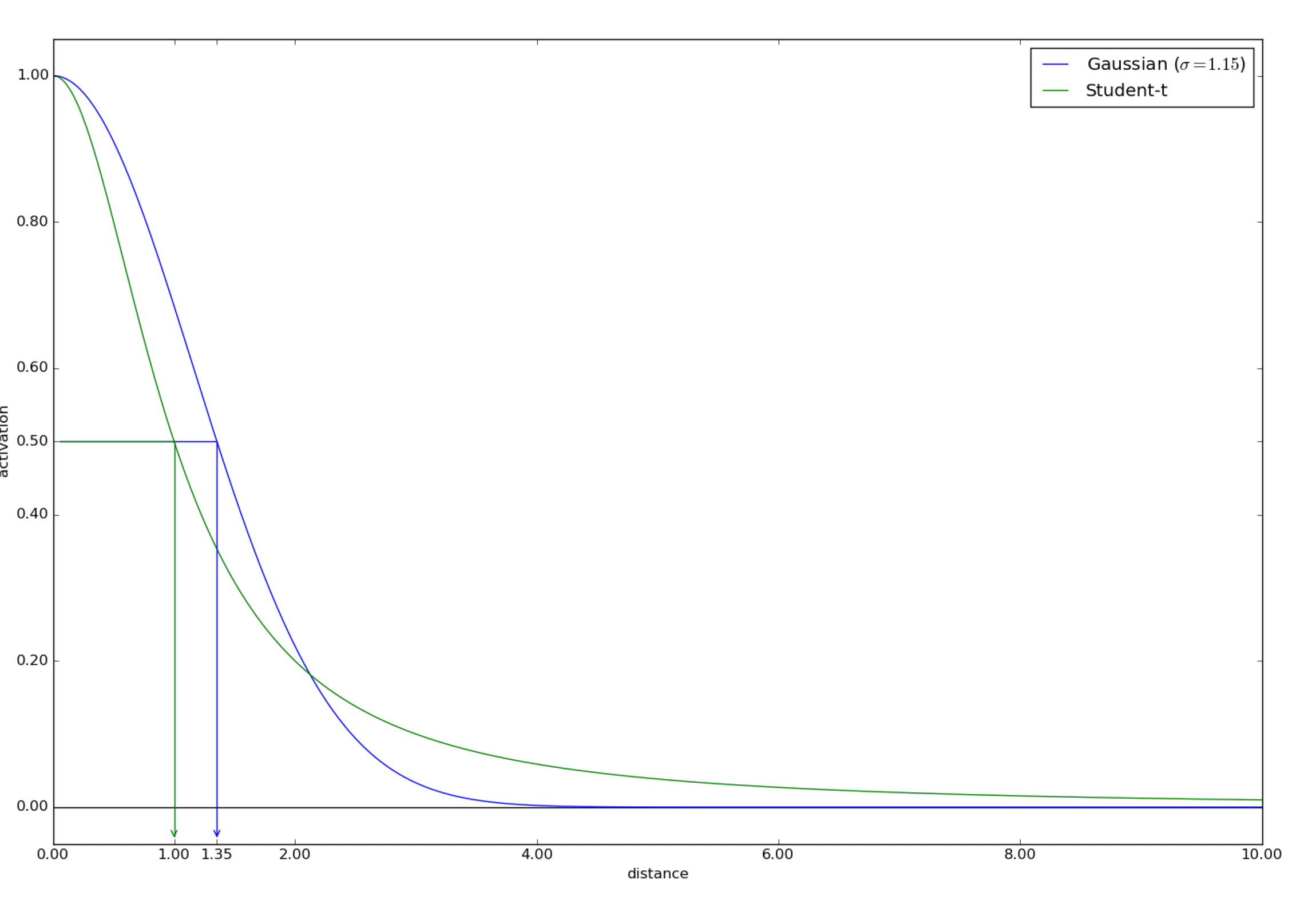
Image("tsne2.png", width=600)

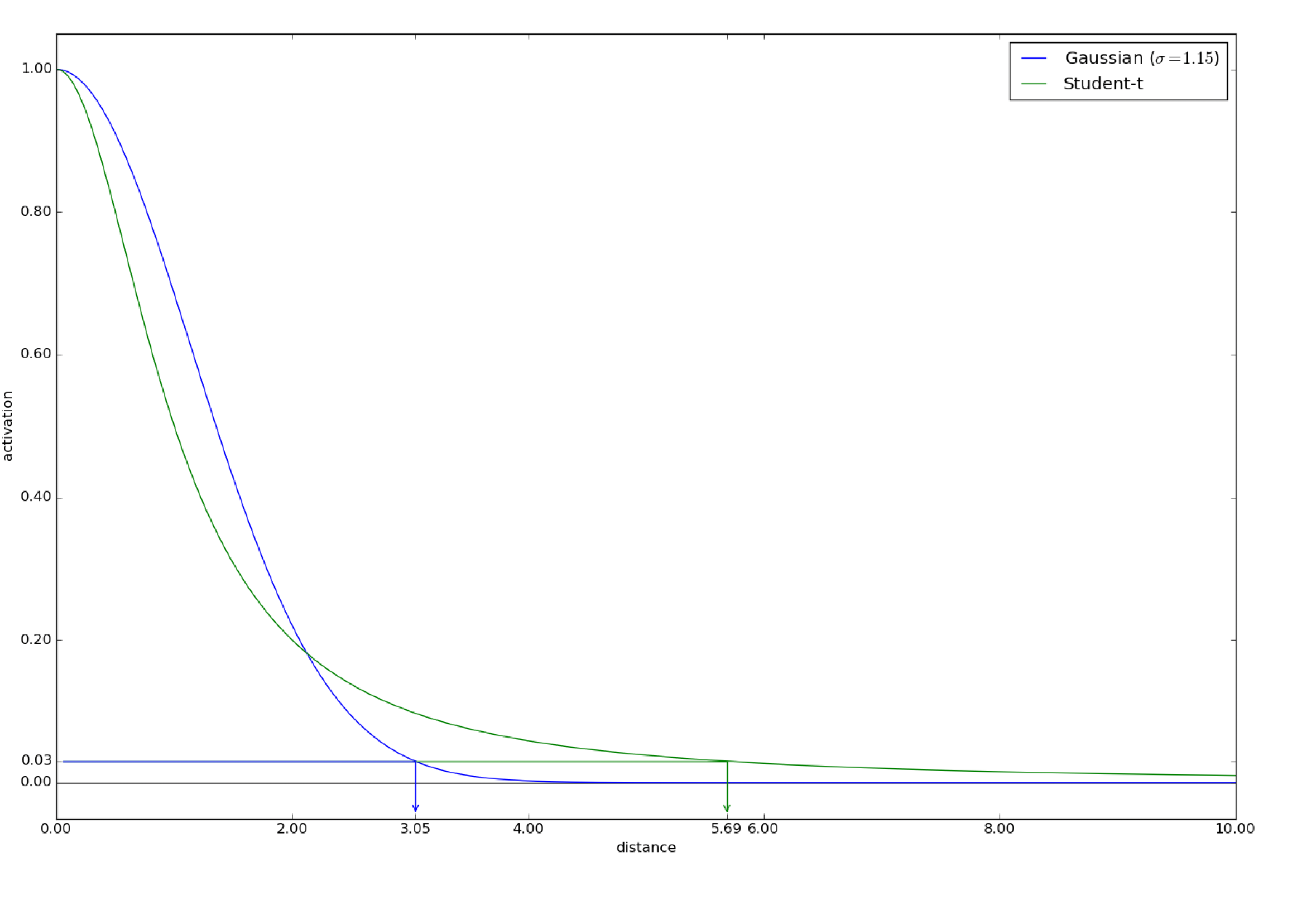
첫 번째 그림에서 보면 고차원(정규분포, 파란색 그래프)에서 거리가 1.35일 경우 그 확률은 0.5로 나타나서 저차원(t-분포,초록색 그래프)에서는 거리가 1.0으로 더 가까이 취급됨을 확인 할 수 있다. 반대로 두 번째 그림에서는 고차원에서 거리가 3.05로 더 멀어진 경우 그 확률은 0.03으로 나타나고 그것에 대응되는 저차원에서의 거리는 5.69로 더 멀어진것을 확인할 수 있었다.

즉 이런식으로 t-분포를 사용함으로써 고차원에서 가까운 경우는 저차원에서 더 가깝게, 고차원에서 멀리 떨어진 경우는 더 멀게 해주는 효과를 얻을 수 있었다. 그래서 $Q$분포를 얻을 때 정규분포에 해당하는 방사기저 커널이 아닌 t-분포에 해당하는 유사도를 사용해 SNE의 crowding problem를 해결 할 수 있다.

4.2. 작동원리

대부분의 원리는 SNE와 동일하고 차이점은 $Q$의 분포를 구하는것에 있어서 방사기저 커널이 아닌 $\frac{1}{1+x^{2}}$을 사용하는것에 있다. 왜냐면 4.1.의 첫번째 그림에서 확인할 수 있듯이 t-분포가 해당 식에 비례하기 때문에 $\frac{1}{1+x^{2}}$을 사용한다. 이를 사용함에 따라 확률이 0에 더 천천히 다가가는 효과를 줄 수 있다. t-SNE에서 새롭게 정의된 $Q_{ij}$는 다음과 같다.

\[Q_{ij} = \frac{(1 + \|y_{i} - y_{j}\|^{2})^{-1}}{\sum_{k}\sum_{l \neq k}{(1 + \|y_{k} - y_{l}\|^{2})^{-1}}}\]

이때 $P_{ij}$는 SNE에서 정의된 것과 동일하고 이것들은 symmetric한 버전임에 주의하자.

이때 마찬가지로 loss function을 KL divergence로 정의하고 $y_{i}$에 대한 gradient를 구해보면 다음과 같다.

\[\frac{\partial C}{\partial y_{i}} = 4 \sum_{j}{(P_{ij} - Q_{ij})(y_{i} - y_{j})}(1 + \|y_{i} - y_{j}\|^{2})^{-1}\]

이와 비교하기 위해서 symmetric SNE의 symmtric한 버전의 gradient를 구하면 다음과 같다.

\[\frac{\partial C}{\partial y_{i}} = 4 \sum_{j}{(P_{ij} - Q_{ij})(y_{i} - y_{j})}\]

이를 보면 두개의 차이점은 $(1 + |y_{i} - y_{j}|^{2})^{-1}$ 이 곱해진것인데 이를 통해서 거리가 멀면 weight(gradient)가 줄어들어서 더 끌어당겨서 군집으로 만드는 힘이 약해진다고 이해할 수 있다. 이를 통해서 거리가 멀면 저차원공간에서 멀리 떨어져 있게 함으로써 crowding 문제를 해결했다.

4.3. 주의사항

위와 같은 방식을 통해서 t-SNE는 몇백 심지어 몇천 차원의 공간도 2차원공간으로 축소시켜 시각화 할 수 있게 해주는 놀라운 기능을 가졌지만, 몇 가지 주의해야 할 사항이 있다. 해당 내용들은 “How to Use t-SNE Effectively(https://distill.pub/2016/misread-tsne/)에서 참고했다.

• 여러 perplexity값에 대해서 시행하라.

Image("sne1.png", height=100)

위의 경우와 같이 T-sne는 서로 다른 perplexity에 대해서 상당히 다른 결과값을 얻을 수 있다. 보통 5-50 사이일때 robust하며 좋은 결과를 얻는다고 알려져 있다. 그래서 해당 값들로 반복해서 수행하는 것이 추천된다.

• 군집이 안정될 때까지 반복해라

Image("tsne3.png", height=100)

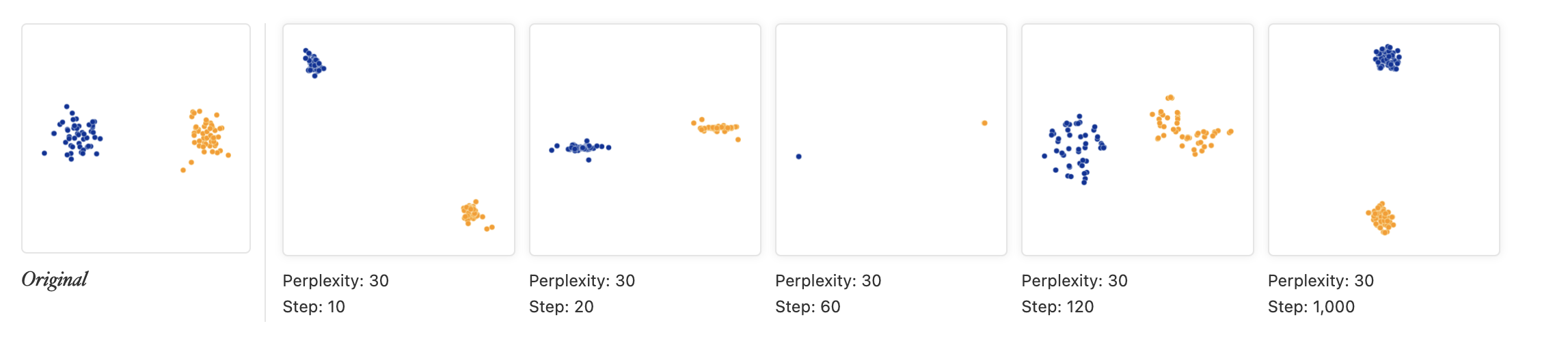
위의 경우와 같이 같은 perplexity 값에 대해서 시행하는 동안 군집이 바뀌고 섞일 수 있으므로 충분한 반복횟수를 줘야하는것이 중요하다. 다만 반복횟수의 경우 정해진 것은 없고 데이터마다 다른것에 주의해야 한다.

• t-SNE의 결과로 나온 군집의 크기는 의미가 없다.

t-SNE의 결과로 도출된 저차원에서의 데이터 군집의 크기(sample size가 아니라 분산의 크기로 이해하면 될 것 같다)는 실제 데이터셋에서 각 군집의 크기와 관련이 없음에 유의해야 한다. 다음 그림을 보면,

Image("tsne4.png", height=100)

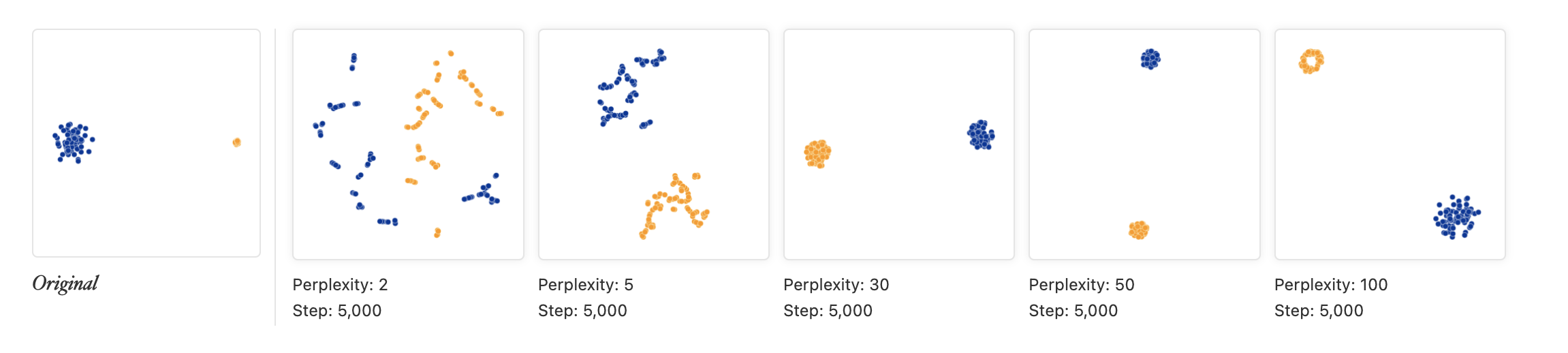
perplexity가 5, 30, 50인 경우 주황색점과 파란색점의 분포의 크기는 거의 비슷하게 나타나지만 실제 데이터에서는 파란색점의 분포의 크기가 훨씬 큼을 확인할 수 있다. 여기서 우리는 저게 실제로 2차원인 경우라 원래 데이터셋을 산점도로 찍어볼수있지만 실제로는 제일 왼쪽의 결과는 모른다고 봐야한다. 저걸 모를때 오른쪽것들의 결과만 보고 “아 주황색 분포와 파란색 분포의 크기는 거의 유사하구나” 이렇게 해석할시에 정말 큰 일이 날수 있으니 주의하도록 하자.

• t-SNE의 결과로 나온 군집사이의 거리는 의미가 없다.

위에서의 내용과 유사하게 t-SNE의 결과로 나타난 저차원 공간에서 군집사이의 거리는 실제 데이터셋에서 군집사이의 거리에대한 정보를 주지 않는다.

Image("tsne6.png", height=100)

이와 같이 실제 데이터셋에서는 파란색 군집과 주황색 군집이 서로 가까이 있고 초록색 군집은 혼자 멀리 떨어져있찌만 t-SNE의 결과로 나온 저차원 데이터 공간에서는 세 집단의 거리가 거의 동일하게 표현됨을 알 수 있다. 모든 경우 이런것은 아니지만 이렇게 나타나는 경우가 있으니 섣불리 t-SNE 결과만을 보고 각 군집사이의 거리를 판단하면 안된다.

• t-SNE는 에러를 에러로써 보지 못할 수 있다.

Image("tsne7.png", height=100)

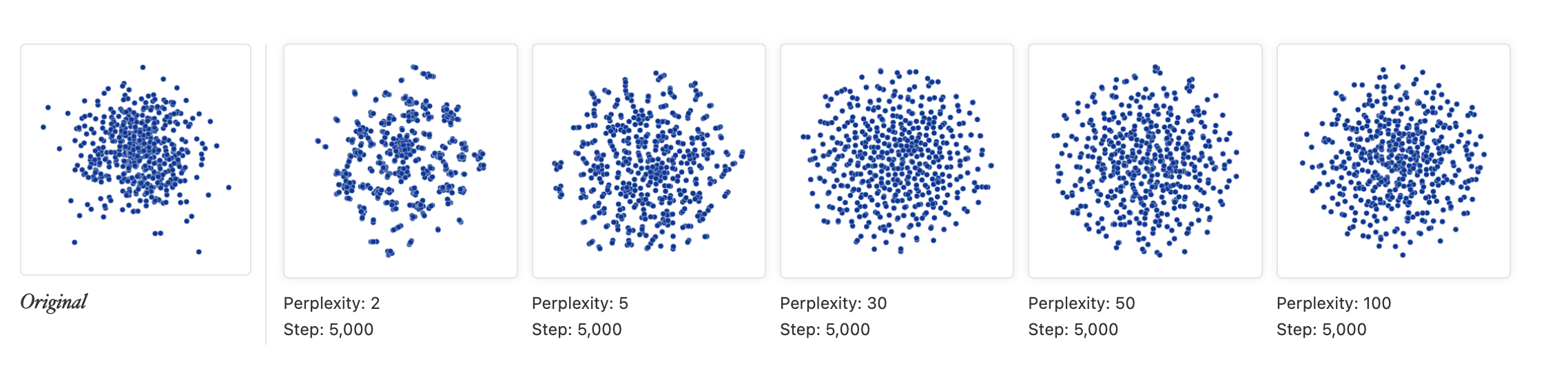
위의 그림은 100차원 정규분포에서 500개의 점을 뽑아 처음 두개의 차원만을 사용해서 점을 나타낸 것이다. 이 때 perplexity가 2인 경우 접들이 어느정도 산포를 이루고 있는 것을 볼 수 있는데 실제로 저 점들은 아무런 규칙도 없는 랜덤에러들이다. 이처럼 t-SNE를 사용할 때 랜덤데이터를 패턴이 있는 데이터처럼 생각하는 함정에 빠지지 않도록 주의해야 한다.

• t-SNE를 사용할때 여러가지 perplexity 값에 대해서 시행해 보고, 여러개의 결과값을 구해봐라.

다음 데이터셋은 50차원 정규분포에서 평균은 동일하지만 주황색 점의 표준편차가 파란색점 보다 50배 더 큰 경우에서 75개의 점을 생성해 두개의 축만 사용해서 점을 찍은 경우이다.

Image("tsne8.png", height=100)

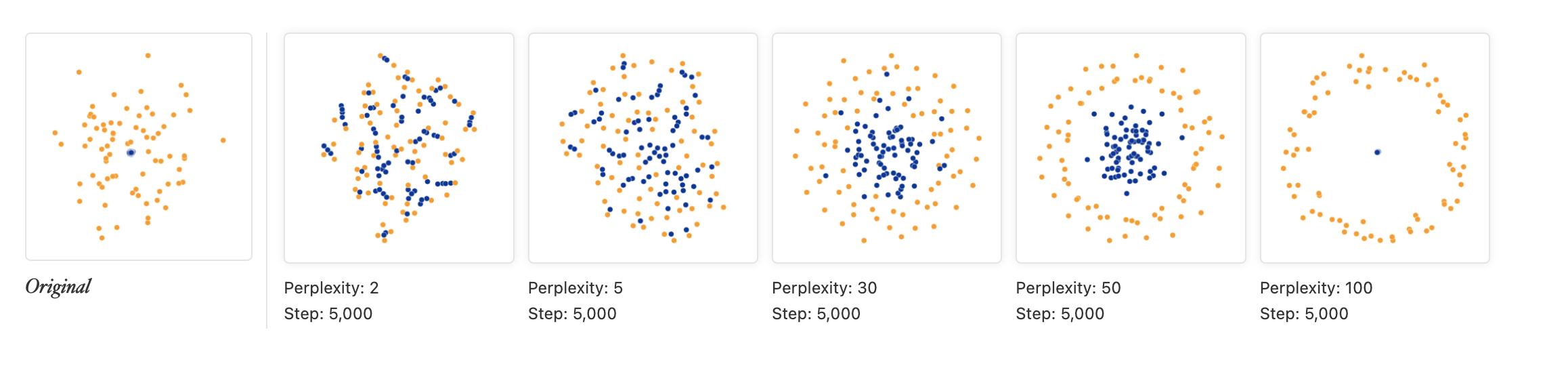
이 경우 perplexity가 30일 때 저런 경향성을 잘 잡아냈지만 보면 perplexity가 50이거나 100일때 주황색점이 아에 파란색 점을 포위하도록 점들이 찍히는데 실제로는 저렇게 까지 극단적으로 데이터가 분포되있지 않음을 주의해라. 그래서 여러가지 perplexity 값에 대해서 t-SNE를 시도해보는게 도움이 된다.

또한 같은 perplexity 값일지라도 각 시행할때마다 다른 결과가 나오는 경우도 있다.

Image("tsne9.png", height=100)

이와 같은 경우 perplexity값은 2로 동일하고 5000번 반복해서 분포가 수렴할때까지 시도했지만, 모든 결과가 다 다르게 도출된 것을 알 수 있다. 이런 경우 때문에 t-SNE는 반복해서 시행해 보는것이 도움이 될 것이다.

지금까지 t-SNE의 아이디어와 그 구동방식 그리고 사용시에 주의해야할 사항에 대해서 알아봤다. t-SNE는 고차원 데이터셋을 저차원으로 차원축소시켜 시각화하는 효율적인 방법이지만 그것을 사용할 때 몇가지 유의사항을 생각하고 있으면 더 효율적인 데이터 분석이 가능할 거라 생각한다. 다음에는 간단한 예시코드를 통해 t-SNE를 실제로 어떻게 구현하는지 살펴보로독 하자.

4.4 예시 코드

t-SNE는 scikit-learn의 manifold에 내장되있어 해당 모듈을 불러와서 사용하면 된다. R에서는 tsne 패키지로 사용할수 있다고하나 sparse matrix를 고려하지 않아서 구동시에 데이터의 크기가 커지면 필요한 메모리가 너무 많아져 잘 작동하지 않는 경우가 있다고 하니 주의하도록 하자. 이번에는 python에서 sklearn을 사용한 코드를 알아보도록 하자. 시뮬레이션 데이터는 sklearn에 내장되어 있는 반달 데이터를 사용하였다. 이 때 여러가지 perplexity 값을 사용해서 각 경우에 어떻게 되는지 산점도를 찍어보았다.

from sklearn.datasets import make_moons
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
import numpy as np


X, y = make_moons(n_samples=100, random_state=123)


tsne = TSNE(n_components=2, perplexity=2)
X_tsne_2 = tsne.fit_transform(X)

tsne = TSNE(n_components=2, perplexity=5)
X_tsne_5 = tsne.fit_transform(X)

tsne = TSNE(n_components=2, perplexity=30)
X_tsne_30 = tsne.fit_transform(X)

tsne = TSNE(n_components=2, perplexity=50)
X_tsne_50 = tsne.fit_transform(X)

tsne = TSNE(n_components=2, perplexity=99)
X_tsne_99 = tsne.fit_transform(X)


fig, ax = plt.subplots(nrows = 1, ncols =6, figsize = (50,8))

ax[0].scatter(X[y==0, 0], X[y==0, 1],
            color = 'red', marker = '^', alpha=0.5)
ax[0].scatter(X[y==1, 0], X[y==1, 1],
            color = 'blue', marker = 'o', alpha=0.5)

ax[1].scatter(X_tsne_2[y==0, 0], X_tsne_2[y==0 , 1],
        color='red', marker = '^', alpha = 0.5)
ax[1].scatter(X_tsne_2[y==1, 0], X_tsne_2[y==1 , 1],
        color='blue', marker = 'o', alpha = 0.5)

ax[2].scatter(X_tsne_5[y==0, 0], X_tsne_5[y==0 , 1],
        color='red', marker = '^', alpha = 0.5)
ax[2].scatter(X_tsne_5[y==1, 0], X_tsne_5[y==1 , 1],
        color='blue', marker = 'o', alpha = 0.5)

ax[3].scatter(X_tsne_30[y==0, 0], X_tsne_30[y==0 , 1],
        color='red', marker = '^', alpha = 0.5)
ax[3].scatter(X_tsne_30[y==1, 0], X_tsne_30[y==1 , 1],
        color='blue', marker = 'o', alpha = 0.5)

ax[4].scatter(X_tsne_50[y==0, 0], X_tsne_50[y==0 , 1],
        color='red', marker = '^', alpha = 0.5)
ax[4].scatter(X_tsne_50[y==1, 0], X_tsne_50[y==1 , 1],
        color='blue', marker = 'o', alpha = 0.5)

ax[5].scatter(X_tsne_99[y==0, 0], X_tsne_99[y==0 , 1],
        color='red', marker = '^', alpha = 0.5)
ax[5].scatter(X_tsne_99[y==1, 0], X_tsne_99[y==1 , 1],
        color='blue', marker = 'o', alpha = 0.5)

ax[0].set_xlabel("Orginal")
ax[1].set_xlabel("Perplexity: 2")
ax[2].set_xlabel("Perplexity: 5")
ax[3].set_xlabel("Perplexity: 30")
ax[4].set_xlabel("Perplexity: 50")
ax[5].set_xlabel("Perplexity: 99")

plt.show()

이 예시의 경우 원래 데이터가 비선형인 경우인데 이런 경우에도 t-SNE가 두 집단을 잘 구분함을 확인할 수 있었다. 특히 여러 perplexity값으로 시도해 봤을때 perplexity가 5인 경우에 두 집단을 특징적으로 잘 구분해냄을 볼 수 있었고, 주의해야할 점은 총 데이터의 개수가 100개 이므로 perplexity를 100이상으로 할 수 없어서 제일 큰 값을 99로해서 시도해 봤다. 지금은 간단하게 예시를 들기 위해서 원래 데이터셋도 2차원 공간이지만, 실제로는 이런경우가 아니라 수십, 수백 차원을 가지는 데이터에 적용됨을 생각하면 좋을것 같다.

5. 결론

지금까지 차원축소 방법인 t-SNE에 대해서 살펴봤다. t-SNE는 차원축소를 통해서 시각화를 하는 방법으로 주성분에 투영을 해 차원축소를 하는 주성분 분석과 달리 저차원에서의 다양체를 학습해 차원축소를 진행한다. 이 때 저차원 공간에서는 t-분포를 사용해 각 점들의 거리를 측정하고 이와 원래 공간에서의 거리를 비교한 KL-divergence를 사용해 손실함수를 만들고 이를 경사하강법을 통해 최소화 해가는 과정에서 저차원 공간을 학습한다. 그리고 t-SNE를 사용할 때 주의해야 할 점들에 대해서 알아봤고 python에서 예시코드도 살펴봤다. 데이터 분석에 실제로 들어가기전 PCA나 t-SNE와 같은 방법을 사용해 미리 데이터셋을 한번 시각화하고 분석에 들어가면 더 좋을거라 생각한다.

실제 t-SNE를 공부해봐야 겠다 생각한것은 이전에 model interpretability를 공부할때 post-hoc 방법의 한 종류로써 사용될 수 있다는걸 보고 본격적으로 공부해보고 싶다고 생각을 했었다. 다만 그 내용까지 다루기엔 너무 내용이 많아질것 같아 추후에 따로 다뤄보고 싶다. 그뿐 아니라 t-SNE와 주성분분석을 비교한 내용들도 있던데 이 또한 알아보면 좋을것 같고 UMAP이라는 다른 다양체 학습법과도 많이 비교되던데 UMAP이 성능적으로 더 우월하단 말이 있어 그 역시 공부해보고 싶다는 생각을 했다.

6. 참고자료

1. Van der Maaten, Laurens, and Geoffrey Hinton. "Visualizing data using t-SNE." Journal of machine learning research 9.11 (2008).
2. Hinton, Geoffrey E., and Sam Roweis. "Stochastic neighbor embedding." Advances in neural information processing systems 15 (2002).
3. Wattenberg, et al., "How to Use t-SNE Effectively", Distill, 2016. http://doi.org/10.23915/distill.00002
4. https://scikit-learn.org/stable/modules/generated/sklearn.manifold.TSNE.html